In my electronic engineer profession, often times I have to use one of these state variable filters. These are actually specific types of active filters that are used in electronic circuits. These are built using one or more integrators positioned in a certain feedback arrangement. Whenever We have the requirement for an exact quality factor (Q factor) output, which might be difficult to accomplish with conventional multi-order filters, this state variable filter configuration appears to be helpful.
Getting Precision in Q Factor Control
We are able to practically regulate the Q factor of the filter with great accuracy thanks to a state variable filter. In applications where exact frequency selection and stability are critical, this is important. A popular way of building a state variable filter is to add the integral and double integral of the input signal. This setup helps in preserving the filters accuracy and producing the required frequency response characteristics.
Alternative way to Implement MDAC
As an alternative, We may use Multidimensional Analog Computation (MDAC) for building a state variable filter circuit. Depending on the specific requirements of the circuit, this approach may provide more flexibility and performance advantages. With this we can optimize the filter for a variety of applications by selecting the best implementation, making sure that we fulfill all performance requirements and get the desired results from signal processing.
Understanding Kerwin-Huelsman-Newcomb (KHN) biquad filter Circuit
In my audio related experiments I frequently utilize the Kerwin-Huelsman-Newcomb (KHN) biquad filter as an example of a flexible filter construction. This filter is significant because it can output lowpass, highpass, and bandpass signals from a single input. It is a second-order filter, sometimes known as a biquad filter.
Derivation and Structure of the KHN Biquad Filter
The KHN biquad filter was designed using an innovative derivation technique. It begins with the transfer function of a high-pass filter which is defined as the ratio of two quadratic functions. By rearranging this transfer function, We observe a structure that resembles a state-variable filter circuit design. The rearrangement demonstrates that, one of the output signals is effectively the sum of integrated reproductions of the input signal. This is the distinguishing characteristic of state-variable filters.
KHN Biquad Filter Circuits are Versatile
Referring to the following circuit diagram, by configuring the various states in the filter circuit we are able to achieve many different kinds of filters from a same configuration. For example, the KHN biquad filter enables us to generate lowpass (LP), highpass (HP), and bandpass (BP) responses all from a single input signal, denoted as Vin in the design. This versatility is really useful in situations where We need to extract various frequency components from a single data channel.
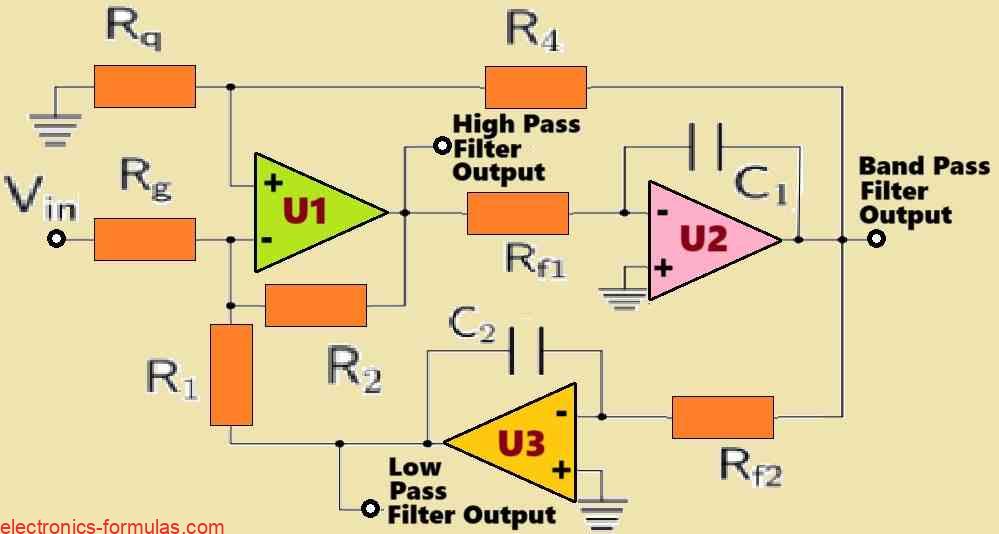
Understanding the Formulas
To make the formulas and the calculations simple, we set:
Rf1 = Rf2
C1 = C2
R1 = R2
Then, the cut-off frequency can be found using the following formula:
Q = (1 + R4/Rq)(1/(2 + (R1/Rg))
For the low-pass filter (LP) and the high-pass filter HP) outputs, the gain of the pass-band can be calculated using the following formula:
AHP = ALP = R1/Rg
From the above data we can see that, both, the cut-off frequency and the Q factor can be adjusted independently. This flexibility of this design, along with the ability to switch between different filter responses, makes state-variable filter circuits extremely popular in analog synthesizers applications.
If we assume the resonance frequency to be of 1 kHz, then the values of the various components in the circuit can be selected in the following manner:
Rf1 = Rf2 = 10k,
C1 = C2 = 15nF
and R1 = R2 = 10k
Extending Filter Orders with State Variables
In more complicated state-variable filter circuit designs, higher filter orders can be achieved by including extra integrators that correspond to more states. This means that We can modify the filter’s performance to match individual needs, whether it is a basic biquad filter or a more complicated filter with extended order.
Applications
State variable filters are widely used in electronics to modify the frequency response in applications involving audio signal processing. Because the frequency, Q factor, and filter type may all be separately controlled, these filters are extremely versatile and can be used for a wide range of applications.
We frequently utilize these filters in parametric equalization circuits when we setup them with low Q levels. In this case, we may precisely modify particular frequency bands, which assists in shaping the tonal balance of the audio signal. The low Q setting makes sure that we can adjust frequencies in a wide and seamless manner, which is perfect for slight modifications to the audio spectrum.
On the other hand, we find that these filters work particularly well for building resonant filter modules in analog synthesizers when we set them to high or variable Q values. By emphasizing particular frequencies, we may create distinct peaks or notches in the frequency response by adjusting the high Q values. This characteristic is essential for our synthesizers to produce dramatic sound effects and rich, resonant tones.
In instances where we need a manual frequency adjustments, we can use a dual potentiometer in place of the resistors Rf1 and Rf2. With this tweak we can easily and quickly manually alter the frequency response of the filter.
When we require voltage control instead of manual adjustment we can substitute the operational amplifiers U2 and U3 with voltage-controlled amplifiers (VCAs) or operational transconductance amplifiers (OTAs). These components will enable us to control the filter parameters via voltage signals, facilitating automated or remote adjustments of the filters frequency and Q factor. This is particularly useful in advanced audio processing systems and synthesizers.
Conclusion
Thus it looks like the the adaptability of state variable filters in various configurations makes them a powerful tool for shaping audio signals, whether we are performing real-time sound manipulation or whether implementing automated control systems.
Source: https://en.wikipedia.org/wiki/State_variable_filter
Leave a Reply