We usually think of decibels as being used to measure loudness. But when designing amplifier and filter circuit layouts, we typically come across numerical values that have extremely wide ranges. For example, a total gain of 665 (19 multiplied by 35) is obtained through cascading two amplifier stages with power gains of 19 and 35 respectively. Similar to this, a total attenuation of 0.5 (0.7071 into 0.7071) is obtained by cascading two first-order RC filter circuits with respective attenuations of 0.7071. It is important to keep in mind that although negative outputs denote attenuation or loss, positive outputs indicate amplification or gain.
You may realize that it can be more helpful to compare output-to-input amplitude ratios on a logarithmic scale rather than a linear one when doing circuit analysis in the frequency domain. By using the logarithmic ratio of two numbers, P1 and P2, a new decibel level is introduced.
In contrast to voltage and current, which are expressed in volts and amperes respectively, the decibel, or simply dB, is only a ratio of two numbers. It is in fact just the ratio of one value to a specific or well-known reference value. Therefore the decibel has no dimensions, instead, it is named after Alexander Graham Bell and is represented by the unit “Bel”.
Decibels (dB) can be used to express any pair of values as long as they have the same number or units (power, voltage, or current). A “deci” indicates one-tenth (1/10th) of a Bel. As a result we have 10 decibels (10dB) per Bel, or one Bel = 10 decibels.
Decibels are a common unit of measurement that we use to express variations in power level, either increasing or decreasing. We normally employ the following terminology: ten times the base-10 logarithm of two power levels.
As an example, the power ratio of one watt to ten watts is the same as the power ratio of ten watts to one hundred watts, both amounts to a 10:1 ratio. Despite there is a significant numerical difference between 9 and 90 watts, the decibel ratio stays the same.
It is critical to understand that the decibel (dB) number does not indicate power, rather it is a ratio that is used to compare and evaluate the level changes in power. The formula for the decibel ratio of two power numbers, P1 and P2, is given as:
dB = 10log10[P2/P1]
Here P1 and P2 stand for input and output power respectively, generating the power ratio (POUT/PIN). Because the decibel measures the base-10 logarithmic difference between two power levels, we may use antilogarithms to further clarify this connection and find the exact value of a one-decibel (1dB) change.
Using the equation dB = 10log10[P2/P1], we may investigate the case in which P2/P1 = 1, which suggests that P1 and P2 are equal. This results in:
dB = 10log10[1] = log10[1/10] = log10[0.1] = antilog[0.1]
So this implies that a change in the dB value becomes equivalent to 100.1, or around 1.259.
Now it is obvious that the logarithmic power ratio represents a factor of 1.259. This means that a change in power of 1dB corresponds to an increase (or decrease) of around 25.9% (rounded to the nearest to 26%).
For example when we increase a circuit or system’s gain by 26% from 5 (or 7dB) to 6, the resulting power ratio is 5 * 1.26 = 6.3. When we translate this back to decibels we get 10log10(6.3) = 8dB. This indicates an increase in gain of +1dB which confirms that a change of +1dB translates into a 26% logarithmic power increase, and this change is not linear in nature.
Solving a Decibels Problem #1
We have an audio power amplifier unit which produces 220 watts of power when connected to a load of an 4 ohm speaker through a supply of a 100 mW of input signal. Let us calculate the power gain of this amplifier in decibels.
We can calculate the result by solving the following equation:
Power Gain = Ap = 10 * log10[P2/P1]
Ap = 10 * log10[P2/P1]
= 10 * log10[220/0.1]
= 10 * log10[2200]
= 33.42 dB
Calculating the Maximum Input Audio Power of an Amplifier, using its dB Gain:
The power gain of an amplifier can be expressed in dB, regardless of the amount of its input or output power values. Using the above explained information for instance, an amplifier with a power gain of 33.5 dB could produce 88 watts of output power from a 40 milliwatt input.
By first converting decibels into Bels, remembering that a decibel is one-tenth of a Bel, we could, if wanted, convert this decibel number back to a linear value. Let’s say we have a 220-watt audio amplifier, for example, which has a power gain ratio of 33.5dB. In order to find its maximum input value, we can carry out the necessary calculations, as indicated below:
Ap = 10 * log10[P2/P1] dB
∴ 220/P1 = Anti-logAp/10 = 10(33.5/10) = 2239
∴ 220/P1 = 2239
∴ P1 = 220/2239 = 0.098 watt = almost 100 mW
As we can see, the answer is 100 mW which is exactly the same as calculated in our above problem #1.
Advantage of base 10 logarithm
While working with many amplifier, filter, or attenuator stages which are cascaded together, we find that employing the base 10 logarithm ratio of two powers is really beneficial because it allows us to add or subtract their decibel values without having to multiply or divide their linear values. Stated differently, the total gain (+dB) or attenuation (-dB) of a circuit is the product of all the individual gains and attenuations for all the stages that have connections between the input and output of the amplifier.
For example, suppose a single stage amplifier has a power gain of 30dB and provides a passive resistive network which has an attenuation of 2, before it amplifies the signal again through a second amplifier stage having a gain of 300. The circuit’s total power increase between the input and output, in decibels, then could be calculated in the following manner:
An attenuation of 2 for the passive circuit corresponds to a positive gain of 1/2 = 0.5, meaning that the passive section’s power gain is:
dB Gain = 10log10[0.5] = -3dB (note a negative value)
The second stage amplifier has a gain of 300, thus the power gain of this section is:
dB Gain = 10log10[300] = +24.77 dB. So the net gain of the circuit will be:
30 – 3 + 24.77 = +51.77 dB.
If you want you can simply double check our result of 51.77 dB by multiplying the gains of the individual stages by employing our normal method that we discussed earlier:
We understand that the power gain of 30dB in decibels will be equal to a gain of 1000, because 10(30/10) = 1000. So:
1000 * 0.5 * 300 = 150000
If we convert this back to a decibel value we get the following result:
dB Gain = 10 * log10[150000] = 51.76dB
So now we can clearly see that a gain of 150,000 is equivalent to a power gain ratio of +51.76 dB, as previously demonstrated, indicating that we can represent extremely high power ratios using decibel values that are considerably lower in magnitude since, for example, 51.76 dB is a power ratio of 150,000, whereas -51.76 dB corresponds to a power ratio of 0.0000066. Thus, the math becomes a little bit simpler when we use decibels in the calculations.
How to Calculate Decibels of Voltage and Current
Assuming we know the value of the resistance, then we can represent any magnitude of power as a voltage or current. We know as per Ohm’s P = V2/R and P = I2R, therefore because V and I correspond to the current flowing through and the voltage through the same resistance, the dB values for the voltage (V1, and V2) and current (I1, and I2) ratios can be calculated as follows, specifically if we set R = R = 1.
dBV = 10 * log10[(V22/R)/(V12/R)] = 10log10[V22/(V12]
10log10[V22/(V12] = 10log10[V2/(V1]2
∴ dBV = 10log10[V2/(V1]2 = 20log10[V2/(V1]
which corresponds to 20log(voltage gain).
Now, for the current gain the calculations would be in the following manner:
dBi = 10 * log10[(I22/R)/(I12/R)] = 10log10[I22/(I12]
10log10[I22/(I12] = 10log10[I2/(I1]2
∴ dBV = 10log10[I2/(I1]2 = 20log10[I2/(I1]
Thus we see that in decibel (dB) calculations for power, voltage, and current, the main difference is the use of constants 10 and 20. In order to obtain a valid dB ratio, it is very important to ensure that the two quantities being compared are expressed using the same units, such as watts, milliwatts, volts, millivolts, amperes, milliamperes, or any other consistent measurement.
Solving a Decibel Related Problem #2
Let us consider this situation in which a passive resistive network delivers an attenuation of 12 dB when the input supply voltage is 15 V. We need to find out the magnitude of the output voltage of the network.
dB = 20 * log10[Vout/Vin]
-12 = 20 * log10[Vout/Vin]
-0.6 = log10[Vout/15]
10(-0.6) = Vout/15
0.2512 = Vout/15
Vout = 0.2512 * 15
∴ Vout ≈ 3.768
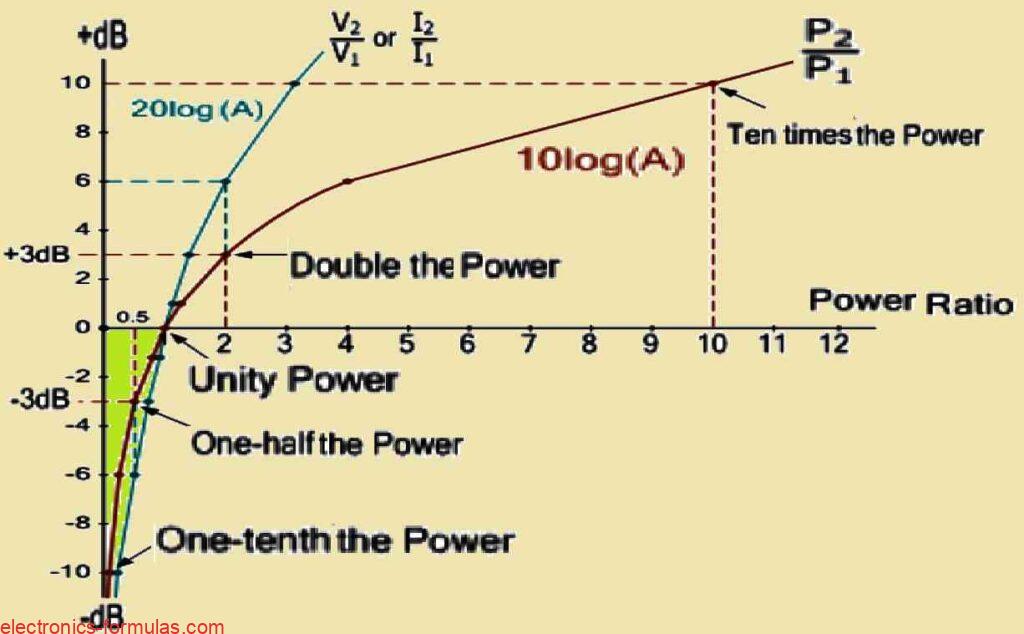
As it is now evident to us that decibels measure logarithmic changes in power, voltage, or current, therefore it is now possible for us to create a table which will illustrate the corresponding gains and their corresponding decibel values.
| dB Value | Power Ratio 10log(A) | Voltage/Current Ratio 20log(A) |
| -20dB | 0.01 | 0.1 |
| -10dB | 0.1 | 0.3162 |
| -6dB | 0.25 | 1/2 = 0.5 |
| -3dB | 1/2 = 0.5 | 1/√2 = 0.707 |
| -1dB | 0.79 | 0.89 |
| 0dB | 1 | 1 |
| 1dB | 1.26 | 1.1 |
| 3dB | 2 | √2 = 1.414 |
| 6dB | 4 | 2 |
| 10dB | 10 | √10 = 3.162 |
| 20dB | 100 | 10 |
| 30dB | 1000 | 31.62 |
Looking at the above given decibel table we see that power, voltage, and current have gain ratios of precisely “1” (unity) at 0 dB. This indicates that there is no gain or loss introduced between the input and output signals by the circuit or system. In simple terms, rather than suggesting zero gain, a 0 dB level denotes a unity gain, meaning that the gain factor A is 1.
Additionally, when the decibel number is +3 dB it means that the system’s or circuit’s output is two times as high as the input. When we have the gain factor A which is larger than 1, we get a positive gain or amplification.
On the other hand, the output goes down to half of the input value at -3 dB. When we have a gain factor A that is lower than 1, we get a negative gain or attenuation. Often called the “half-power” point, the -3 dB point is essential for determining the corner frequency in filter circuit networks.
Although a table illustrating power gains against decibels is useful, in real applications that require amplifiers and filters, I as an electronic engineer find that Bode plots, charts, or graphs are far more helpful for displaying the frequency response characteristics of circuits or systems. With the data from the table, We can create a “decibel” Bode plot as shown below which graphically displays the various power levels and their positions thereby offering a better understanding of the circuit’s behavior at different frequencies.
Power Gain Bode Plot
The following bode plot simply proves that there’s no linearity in the power curve rather it bends according to the logarithmic ratio of 1.259.
Conclusions
The decibel (dB) is a Base-10 logarithmic unit of power change, and as we’ve shown in this lesson, it’s equivalent to a 1/10th value of a Bel (1 Bel = 10 decibels, or 1dB = 0.1B), which is without any dimensions.
As we saw above, a 30dB is equal to a power ratio of 1000. Among the most often used decibel values are 3dB, 6dB, 10dB, and 20dB (and their negative counterparts). The decibel makes it possible to describe large ratios of powers through very small numbers. But, that said, a 20dB does not make the power of 10dB two times higher.
The decibel additionally demonstrates that any power adjustment with the identical ratio would result in the same decibel ratio. For instance, increasing power from 2 watt to 4 watts would give you the same power ratio as increasing power from 8 watts to 16 watts, or a +3dB shift. On the other hand, a -3dB change would cause the power ratio to become half.
A positive dB ratio indicates the presence of gain or amplification because the output power exceeds the input power (POUT > PIN). On the other hand, if the dB power ratio is negative, the circuit is experiencing attenuation or loss since the output power will be lower than the input power (POUT < PIN). Hence, it is evident that a power ratio of 0dB indicates neither signal gain nor decrease.
References: Decibel
Leave a Reply