Crest factor is a way to describe a waveform’s shape. It’s calculated by dividing the waveform’s peak value (maximum value) by its RMS value (effective value).
For a perfect sine wave, the crest factor is 1.414. This tells us that sine waves have a predictable peakiness.
Crest factor (CF), also called peak factor or amplitude factor, is a mathematical tool used to analyze various periodic waveforms.
It helps us understand a waveform’s shape by comparing its peak value (highest point) to its RMS value (effective value).
Different waveforms have different shapes, so their crest factors will vary.
Importance of Crest Factor:
Crest factor tells us the maximum voltage an AC circuit experiences. This is important because, for example, capacitors and cables need insulation that can withstand the peak voltage, not just the RMS value.
AC components need to be able to handle the crest voltage, which is higher than the RMS voltage of the applied voltage.
Crest Factor and Sine Waves:
Sinusoidal waveforms are the most common type of waveform used in electrical and electronic engineering.
An alternating sine wave can be described by its maximum value, average value, and RMS value, as shown below.
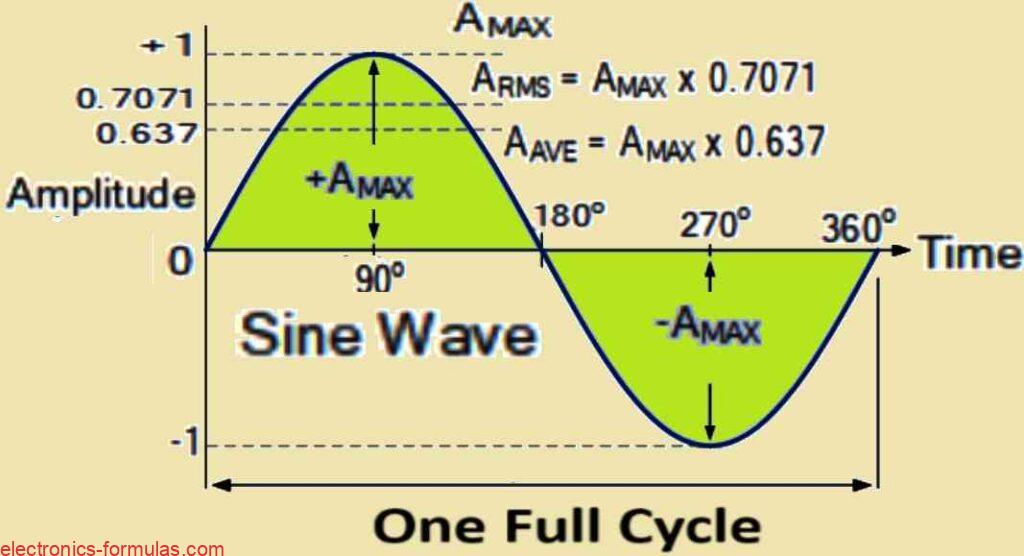
Peak Value (Amax):
The highest point (magnitude) of any waveform is called its peak value or maximum value.
In a sine wave, the maximum positive value (+Amax) occurs at 90 degrees on its cycle.
Conversely, the maximum negative value (-Amax) occurs at 270 degrees.
So, a sine wave has two equal but opposite peak values: +Amax (positive) and -Amax (negative).
RMS Value (Arms):
Since AC waveforms change over time, they don’t have a constant value. The RMS value (Arms) is the equivalent DC value that would produce the same heating effect (I2R) in a resistor.
The RMS value of an AC waveform is calculated for one full cycle and is:
Arms = Amax / √2 = 0.7071 × Amax.
Crest Factor (CF) Formula:
Crest factor (CF) relates the peak value to the RMS value, showing how “peaky” a waveform is.
The formula for crest factor of any waveform is:
Crest Factor = Peak Value / RMS Value
If it is a pure sine wave, then the crest factor may be expressed as:
- CF = Peak Value / RMS Value
- = AMAX / (1/√2)AMAX
- = AMAX / 0.7071AMAX
- = 1 / 0.7071
- = 1.414
Thus, we can see that Crest factor is peak value divided by RMS value. It tells us how big the peaks are compared to average.
Any signal, including a square wave, will have a crest factor greater than 1.
Sharper peaks mean a higher crest factor.
For a perfect sine wave, the crest factor is always 1.414 (square root of 2).
Solving a Crest Factor Problem
Calculate the crest factor of a sine wave, which has a peak value of 310 V.
- CF = VMAX / VRMS
- = VMAX / 0.7071 * VMAX
- = 310 / 0.7071 * 310
- = 1.414
The result simply confirms that it is a pure sine wave.
Solving another Crest Factor Problem
Let’s say an alternating waveform has a peak voltage value of 110 volts and a crest factor of 1.6. How do you calculate its rms value?
- CF = VMAX / VRMS
- ∴ VRMS = VMAX / CF
- VRMS = 110 / 1.6
- VRMS = 68.75 Volts
In the above problem we have used sine waves just as an example. But, crest factor works for any repeating wave shape, including square waves. Frequency, period, and peak all still apply to these waveforms.
Now, square waves are interesting. They can actually be built by adding a bunch of sine waves together. These sine waves would all be odd multiples of the same base frequency.
Understanding Square Wave Crest Factor
Square waves are a unique type of periodic waveform. They constantly switch between two fixed voltages, perfectly balanced around zero.
Unlike some waves, the time spent at each voltage is exactly the same.
This makes them a special case of rectangular waves, with a specific duty cycle of 50%.
Because of these properties, we can still calculate their crest factor just like other waveforms.
Square Wave: Switching Between Positive and Negative Voltages

Why Square Waves Average Out to Zero (But Each Half Doesn’t!)
For most waveforms, the average DC value is found by averaging the area under the curve over one full cycle. However square waves are special. Their positive and negative halves are perfect mirrors of each other, with equal areas. Because of this cancellation, the average value over a whole cycle of a symmetrical square wave is zero.
It’s important to note that this zero average only applies to the full cycle. If we look at just the positive or negative half of the wave by itself, the average value isn’t zero. This is similar to how we analyze sine waves.
For a symmetrical square wave, the average voltage (Vave) during its positive half-cycle is actually equal to its peak voltage (Vmax). That’s because, for that half-cycle, it essentially acts like a constant DC voltage.
Square wave flips between positive peak voltage (+Vp) and negative peak voltage (-Vp) instantly. Squaring this voltage (V2) makes positive and negative values the same.
Because the square wave spends equal time at each peak, averaging the squared voltage (V2) equals the peak voltage squared (Vp2).
For the root-mean-square (RMS) part to hold true, the mean (average) of the voltage squared must also be Vp2. Taking the square root of this mean value (√(Vp2)) is simply Vp.
Therefore, for a symmetrical square wave, the peak amplitude (Vp) and its RMS value (Vrms) are exactly the same: Vrms = Vp.
Since a symmetrical square wave has identical peak (Vp), average, and RMS values, its Crest Factor (ratio of peak to average) becomes:
Crest Factor CF = VPEAK Value / VAVE Value = VPEAK / VPEAK = 1
Symmetrical Square Wave: We observed that the crest factor (peak-to-average ratio) for a symmetrical square wave is simply 1.0 (unity). This makes sense because the peak, average, and RMS values are all identical due to the wave’s flat, symmetrical shape.
Non-Symmetrical Square Waves (Pulse Trains): However things change for non-symmetrical square waves, like pulse trains. How do we calculate the crest factor for these waveforms?
Duty Cycle and Crest Factor:
The crest factor of a series of rectangular pulses (pulse train) is linked to its duty cycle, which is also known as the mark-to-space ratio. Recall that the time for a single complete cycle is called the period (T).
For a pulse train, the duty cycle represents the portion of the period the pulse is “on” (TON) compared to the entire period (TON + TOFF). It’s often expressed as a percentage.
In simpler terms, duty cycle is the ratio of the pulse width to the period. We can express this mathematically: Period (T) equals TON (pulse width) plus TOFF (time pulse is off).

Examples of Duty Cycle:
A pulse with a 15mS “on” time (TON) in a 75mS period (T) has a duty cycle of D = 15/75 = 0.2, or 20%.
Similarly, a pulse “on” for 50mS out of a 75mS period translates to a duty cycle of D = 50/75 = 0.66, or 66%. In this case, the pulse is active for three-quarters of the cycle.
Duty Cycle and Square Waves:
Interestingly, when the “on” time (TON) equals the “off” time (TOFF), the duty cycle becomes 50%, representing a symmetrical square wave. This is because 0.5/1 (TON/T) equals 0.5 or 50%.
General Duty Cycle Formula:
For any pulse train, the duty cycle (D) can be calculated using the following formula: D = TON / T. This takes into account the ratio of “on” time (TON) to the total period (T).
- Duty Cycle (D) = On-time / On-time + Off-time
- = On-time / Period
- = TON / T
For a sine wave, the crest factor is simply the peak value (Vp) divided by its RMS value (Vrms). Following a similar concept, the crest factor of a pulse train with varying duty cycles can be expressed using the formula:
- Crest Factor = √[(1 – Duty Cycle) / (Duty Cycle)]
- = √(1 – D) / D
- Where Duty Cycle (D) = TON / T
In pulse trains, with constant pulse amplitude, the duty cycle plays a major role in determining the crest factor. Imagine three pulse trains with varying duty cycles: 10% (0.1), 50% (0.5), and 90% (0.9). As we’ll see, these duty cycles significantly affect the crest factor.
- When the Duty cycle is 10%
- Crest Factor = √(1 – 0.1) / 0.1 = 3.0
- When the Duty cycle is 50%
- Crest Factor = √(1 – 0.5) / 0.5 = 1.0
- When the Duty cycle is 90%
- Crest Factor = √(1 – 0.9) / 0.9 = 0.33
See how duty cycle affects crest factor in pulse trains. At 10% duty cycle, the train resembles sharp spikes with a high crest factor (around 3.0). The peak voltage is significantly higher compared to the average voltage during the cycle.
Conversely at 90% duty cycle makes the train look like a flat DC level. The crest factor drops significantly (around 0.33). Here, the peak voltage is much closer to the average voltage throughout the cycle as the pulse is “on” for most of the time.
In short, higher duty cycle in a pulse train leads to lower crest factor.
Conclusions
This tutorial explored Crest Factor, the ratio of a wave’s peak value to its RMS value. It reflects the wave’s shape and how closely it resembles a perfect sine wave.
Lower Crest Factor = Better Efficiency
A lower crest factor generally indicates a more efficient power draw from the supply because the peak voltage isn’t significantly higher than the average voltage.
Crest Factor and Power Systems
- Voltage Crest Factor: Indicates the electrical load on the power supply.
- Current Crest Factor: Shows how the load consumes current.
Essentially, crest factor helps assess how connected loads and reactive components impact a system’s power handling capacity. High crest factors can lead to substantial power losses.
Crest Factor and Waveform Types
Different waveforms have varying crest factors based on their peakiness. The more peaked a waveform, the higher its crest factor.
- Symmetrical Square Wave: Crest factor of 1 (unity) due to equal peak and RMS values.
- Pure Sine Wave: Crest factor of √2 (approximately 1.414)
Form Factor Table (provided below)
The following table defines form factor formulas and values for various discussed waveforms.
| Waveform Type | Formula for Crest-Factor | Value |
| Sine Wave | √2 | 1.414 |
| Half-wave Rectified Sine Wave | 2 | 2.0 |
| Full-wave Rectified Sine Wave | √2 | 1.414 |
| Triangle Waveform | √3 | 1.732 |
| Saw-tooth Waveform | √3 | 1.732 |
| Symmetrical Square Wave | 1 | 1.0 |
References: Crest Factor
Leave a Reply