Now let us try to understand this whole thing from very beginning. We are dealing with AC circuits, right? And in AC, we always have these sinusoidal waveforms that keep changing their magnitude and direction with time.
Then to represent both the magnitude and the phase angle of these sinusoidal waveforms, we use something called Phasors.
Now Phasors are nothing but Complex Numbers. These complex numbers help us to show the length of the waveform (its magnitude) and where it is in time (its phase angle). That is why we use them.
But when we are working with AC circuits and frequency-related waveforms then we find that real numbers are not enough. We need something more because AC waveforms have this circular rotation and phase angles which real numbers alone cannot handle.
So that is where Complex Numbers come into the picture. Complex numbers are like an upgrade because they include both real parts and imaginary parts.
Then what is this imaginary number?
In electrical engineering, we always call imaginary numbers using the “j” operator. That “j” just means √-1. We use “j” instead of “i” because “i” is already used for current, so we avoid confusion.
So now if you take some examples, imaginary numbers can be like j3, j12, or j100, all these mean the same as saying 3, 12, or 100 multiplied by √-1.
Then we take a real number like 5 and mix it with an imaginary number like j2 and now we get a complex number, which looks like this:
Z = 5 + j2
Here the 5 is the real part and j2 is the imaginary part.
Now to make sense of all this, we show these complex numbers on a graph. This graph is called a 2D complex plane or s-plane.
In this plane, we draw the real part on the horizontal axis and the imaginary part on the vertical axis.
So like, if we want to show Z = 3 + j4 then we go 3 units right (real axis) and 4 units up (imaginary axis) and that is how we place it on this complex plane.
Now whenever we are dealing with such numbers in DC or AC analysis, we still follow all normal algebra rules.
For example j2 + j4 will become j6, just like 2 + 4 = 6.
But one thing is different. When we multiply imaginary numbers, it behaves differently than real numbers.
Like, j × j = -1
So that means:
j^2 = -1
j^3 = -j
j^4 = +1
j^5 = +j
…and it keeps rotating like this in a cycle of 4.
So every time we multiply by j, it means we are doing a 90 degree anti-clockwise rotation of the vector in the complex plane.
If the result becomes -j then that means we did a 90 degree clockwise rotation.
This whole rotation behavior is very useful in phasor analysis because AC waveforms are also rotating sinusoidals.
Rotation of the vector by the j-operator
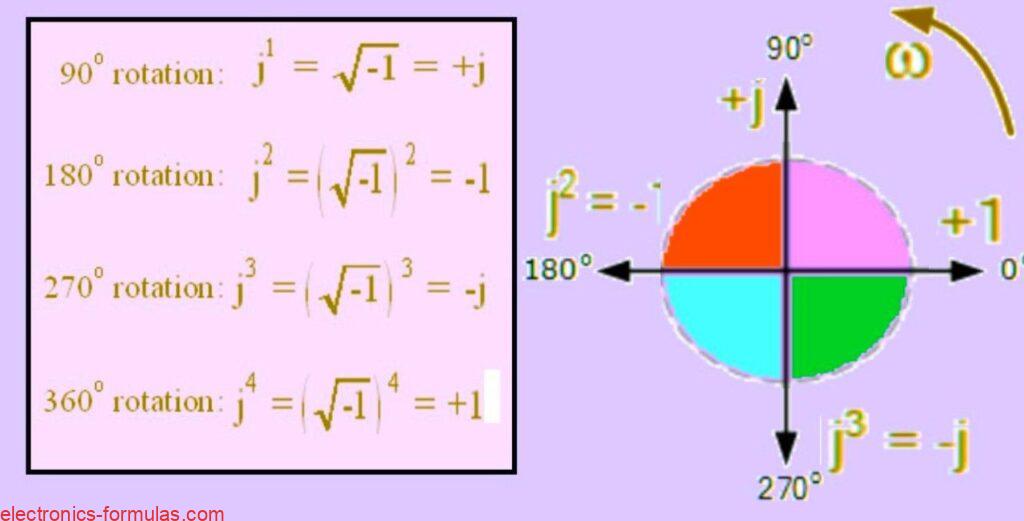
How This j Operator Rotates Vectors and What is Rectangular Form of Complex Numbers.
So we already learned that whenever we multiply something with “j”, it does a kind of anti-clockwise rotation to the vector. Now let us try to see what happens when we multiply with j multiple times.
If we multiply any vector with j² then that vector rotates 180 degrees in the anti-clockwise direction — means it points exactly in the opposite direction now.
Then if we multiply with j³, then vector turns 270 degrees anti-clockwise — like it goes even more and points downwards.
And if we multiply with j⁴, then that means it completes full 360 degrees rotation and comes back to the original direction — like nothing changed.
So now we can say that any time we multiply with j^n, where “n” is some number, then vector will just keep rotating anti-clockwise by 90 degrees multiplied by n.
Like if we do j^10, then vector rotates 10 × 90 = 900 degrees but since 900 is two full circles and a half (2×360 + 180), we get a net rotation of 180 degrees.
Same way for j^30, it rotates 30 × 90 = 2700 degrees but finally lands on some position that is same like j^0, j^1, j^2, or j^3, because this thing repeats in cycles of 4.
So the important thing here is that, only the angle changes, not the length of the vector. That means the magnitude remains same, no matter how many times we rotate it using j.
How we can Show Complex Numbers
In Electrical Engineering there are many ways how we show complex numbers. Some ways are for mathematical solving and some for graphical or visual understanding.
One of the most used and simple way is called the Rectangular Form or also called Cartesian Form. This one uses cosine rule and sine rule and it is very easy to understand.
Now we already saw in the phasor lessons that every complex number is made from 2 parts:
Real part, which we call the active part
Imaginary part, which we call the reactive part
So we can write the complex number like this:
Z = x + jy
Here:
- Z is the full complex number, like a vector.
- x is the real number part (goes on horizontal line).
- y is the imaginary number part (goes on vertical line).
- And j is the imaginary unit which is equal to √-1.
Now when we want to draw this complex number on a graph or plane, then we use something called complex plane or s-plane.
In this plane:
The horizontal line is called the real axis
The vertical line is called the imaginary axis
Let us take an example. Say the complex number is:
Z = 6 + j4
Then we go:
6 units right on the real axis..
4 units up on the imaginary axis.
And where those two meet, that is where the vector Z is located.
Utilizing the complex or s-plane to express complex numbers

How Real and Imaginary Parts Create 4 Quadrants in Complex Plane
So we already saw that in rectangular form, a complex number is made up of two parts, one is real and one is imaginary.
Now one important thing we must remember is that, both these parts, the real one and the imaginary one can be either positive or negative. They are not fixed to be only on right or upward side.
So because of that we cannot just draw the complex number on only positive side of the graph. We have to extend both the axes, the real axis (horizontal) and the imaginary axis (vertical), in both positive and negative directions.
Like :
Real axis must go both right (positive) and left (negative)
Imaginary axis must go both up (positive) and down (negative)
Now when we do this extension, what we get is a complete plane — divided into four sections — and this full layout is called the Complex Plane or sometimes more technically called the Argand Diagram as shown below:
Argand Diagram divided into four quadrants

How Argand Diagram Works with Real and Imaginary Axis and Phasor Rotation
So when we are looking at this Argand diagram then we can clearly see how the axes are arranged.
That horizontal line in the middle, we call it the real axis, this one is showing the positive real numbers on the right side of the vertical axis and also it is showing the negative real numbers on the left side of the vertical axis.
Now the other line, the vertical one which we call the imaginary axis is cutting the real axis right in the middle. And here we find positive imaginary numbers are placed above the horizontal line and negative imaginary numbers are placed below the horizontal real axis.
So because of this full arrangement, we now get a 2-dimensional layout which we call the complex plane. This layout gets divided into 4 parts and we give them names like Quadrant 1 (QI), Quadrant 2 (QII), Quadrant 3 (QIII), and Quadrant 4 (QIV) — just like how we do in normal X-Y graphs.
Now this Argand diagram is not just for showing complex numbers randomly. We also use this diagram to draw a rotating phasor. That means we treat the phasor like a moving point in this complex plane.
The length of the phasor (its magnitude) decides the radius of this rotation. And this phasor keeps rotating around the origin (zero point) and finishes one full circle in 2π divided by ω seconds (which is time period based on angular speed ω).
So once we get this full understanding, we can go one step ahead, we can even use the Argand diagram to understand how a complex number is represented in both rectangular and polar form. Especially when we are focusing on special rotations like 90 degrees turns, then this diagram helps us a lot.
- 0o = ±360o = +1 = 1∠0o = 1 + j0
- +90o = +√-1 = +j = 1∠+90o = 0 + j1
- -90o = -√-1 = -j = 1∠-90o = 0 – j1
- ±180o = (√-1)2 = -1 = 1∠+180o = -1 + j0
Representation of Complex Numbers
So in complex numbers, sometimes we can get values where either the real part or the imaginary part becomes zero. That means we can have something like Z = 6 + j0, here we got real part present but imaginary part is zero or we can have Z = 0 + j4, where real part is zero and only imaginary part is there.
In such cases, we just plot these values directly on the corresponding axis. like, real-only values go on the horizontal axis, and imaginary-only values go on the vertical axis.
How We Calculate Complex Number Angles
Now when we want to know the angle of a complex number then we need to take help of trigonometry, mostly using right-angled triangle concept. Or another way is that we measure the angle anticlockwise from the positive real axis, like we do on the Argand diagram.
Understanding Quadrants and Their Angle Ranges
So this complex plane (Argand diagram) is having four quadrants and each quadrant is having its own angle range.
First Quadrant (I): if the angle is between 0 to 90 degrees, then it falls here.
Second Quadrant (II): if the angle is between 90 to 180 degrees, then it goes here.
Third Quadrant (III): for angles from 180 to 270 degrees, this is the place.
Fourth Quadrant (IV): when the angle is between 270 to 360 degrees, then it lands here.
What is the Formula to Find This Angle
So to find this angle from the real and imaginary parts of any complex number, we use this simple formula:
θ = tan⁻¹ (imaginary part ÷ real part)
But we must also be careful about the quadrant of the number because depending on that, the final angle may need some adjustment (like adding 180 or subtracting something, etc.).
How to Add and Subtract Complex Numbers
Now if we want to add or subtract complex numbers, either mathematically or even using graphs, then we always do it by separating real and imaginary parts.
Like suppose we got two complex numbers A and B, then we just:
Add the real part of A with real part of B.
Then add the imaginary part of A with imaginary part of B.
Same way we subtract also, just subtract real from real, imaginary from imaginary.
So in this way, complex numbers behave just like two-part algebra stuff where we treat real and imaginary parts separately, and still they follow all math rules nicely.
Addition and Subtraction of Complex Numbers
- A = x + jy
- B= w + jz
- A + B = (x + w) + j(y + z)
- A – B = (x – w) + j(y – z)
Example 1: Complex Number Operations
Consider two vectors, A = 4 + j1 and B = 2 + j3. Find the sum and difference of these vectors in rectangular form (a + jb) and represent them graphically on an Argand Diagram.
Mathematical Operations: Addition and Subtraction
How to Add
- A + B = (4 + j1) + (2 + j3)
- A + B = (4 + 2) + j(1 + 3) = 6 + j4
How to Minus
- A – B = (4 + j1) – (2 + j3)
- A + B = (4 – 2) + j(1 – 3) = 2 – j2
Representing Addition, Subtraction through Graph

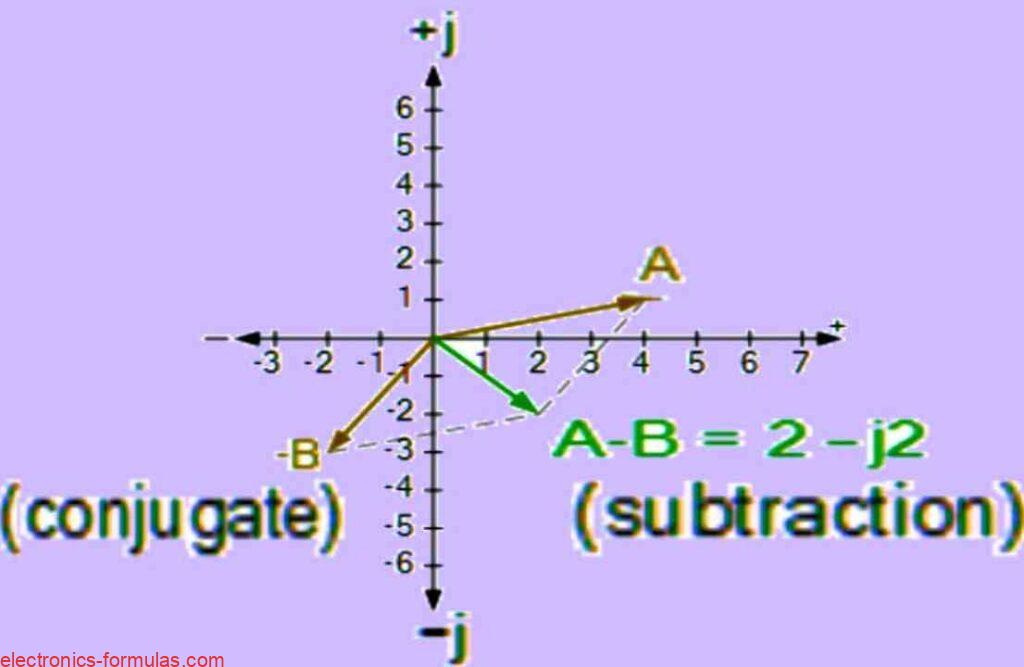
The process of multiplying complex numbers, in rectangular form, adheres largely to the rules of standard algebra, with additional considerations for the consecutive multiplication of the j-operator, where j2 = -1.
To illustrate the multiplication of the two given vectors A = 4 + j1 and B = 2 + j3 yields the following outcome.
- A x B = (4 + j1)(2 + j3) = 8 + j12 + j2 + j23
- However since, j2 = -1
- = 8 + j14 – 3
- A x B = 5 + j14
How We Divide Complex Numbers Using Rectangular Form (Super Crude Way)
So now if we try to divide complex numbers when they are in rectangular form, then that becomes a little tricky — not impossible but little bit harder than addition or subtraction.
Why? Because here we are dividing one complex number by another and in rectangular form, the denominator still has an imaginary part, and we never want to keep imaginary number at the bottom of a fraction.
So what we do? We use a method which is called “rationalizing”. This means that we multiply the top and bottom of the division by the conjugate of the bottom complex number.
What is This Conjugate Thing
Suppose we have a complex number like B = x + jy, then its conjugate will be x – jy. So if our denominator is x + jy, we multiply both numerator and denominator by x – jy.
Why we do that? Because when we multiply a complex number with its conjugate, we get a pure real number at the bottom — like this:
(x + jy) × (x – jy) = x² + y²
That is a real number, no imaginary part left, and now our equation becomes easier to solve.
Polar Form is Easier for Division
But let me tell you, still this whole process in rectangular form is not so smooth. It takes steps and can get messy.
So in electrical engineering, when we want to divide complex numbers easily then we mostly do it by converting them to Polar Form — because in Polar Form, division becomes simple: just divide magnitudes and subtract angles.
But anyway, here we are still doing it in rectangular way.

Understanding Complex Conjugate
So now we come to one very useful idea in complex numbers, this thing is called the complex conjugate or just simply “conjugate”.
Now what is this conjugate? Very simple, we just have to flip the sign of the imaginary part but we keep the real part same like before.
How We Show Conjugate
We normally show the conjugate of a complex number z by putting a small bar on the top of z, like this: z̄.
Suppose we got a complex number like:
z = 6 + j4
Then its conjugate will be:
z̄ = 6 – j4
It is just like that — the real part stays same and the imaginary part changes sign. That means if imaginary part is plus, we make it minus, and if it is minus, then we make it plus.
So if we had:
z = 6 – j4,
then conjugate would be:
z̄ = 6 + j4 As shown in the following diagram
Conjugate Complex Numbers
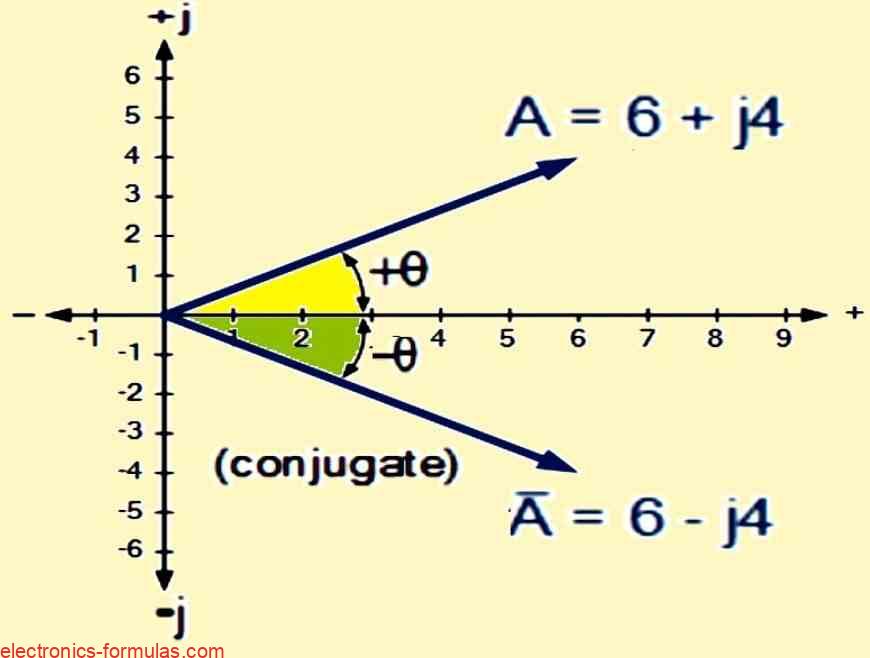
What Happens When We Add or Subtract Complex Numbers and Their Conjugates
So like we already saw before, when we add a complex number with its own conjugate, then something interesting happens, the answer becomes a real number only, no imaginary part at all.
That means when we take a complex number and its mirror version (the conjugate) and then we add them together, then we will only get the real part which is also called the active component.
But if we subtract the conjugate from the original complex number then all the real part cancels out and what is left is only the imaginary part, also known as the reactive component.
Why This is Important in Electrical Engineering
So now in electrical engineering, this idea of complex conjugate is super useful.
Specially when we try to calculate things like apparent power in an AC circuit using rectangular form then this complex conjugate trick becomes really important. Without that we cannot get proper result for power equations.
Now Let us Talk About Complex Number in Polar Form
Ok now we come to another powerful way of showing complex numbers — this is called Polar Form.
In rectangular form, we show complex numbers by x and y coordinates, like real part and imaginary part. But in polar form, we do it in a different way.
Here instead of showing position on a graph, we just say how far the point is (magnitude) and at what angle (argument or phase).
So in polar form, we write it like this:
Z = A ∠±θ
Where:
Z is our complex number in polar form.
A is the modulus or magnitude (how long the vector is).
θ is the angle or argument, which can be positive or negative depending on direction.
What About Its Graph or Triangle View
So when we plot this polar form on paper, we do not use normal square graph, instead we show it as a triangle-style diagram.
This triangle tells us the same story, the length of the vector is A, and its direction from the horizontal real axis is angle θ.
So even though the drawing looks different from rectangular form, the actual magnitude and angle stays exactly same.
That is why both rectangular and polar are just two ways of saying the same thing, like two languages for same number.
Representing Complex Number in Polar Form
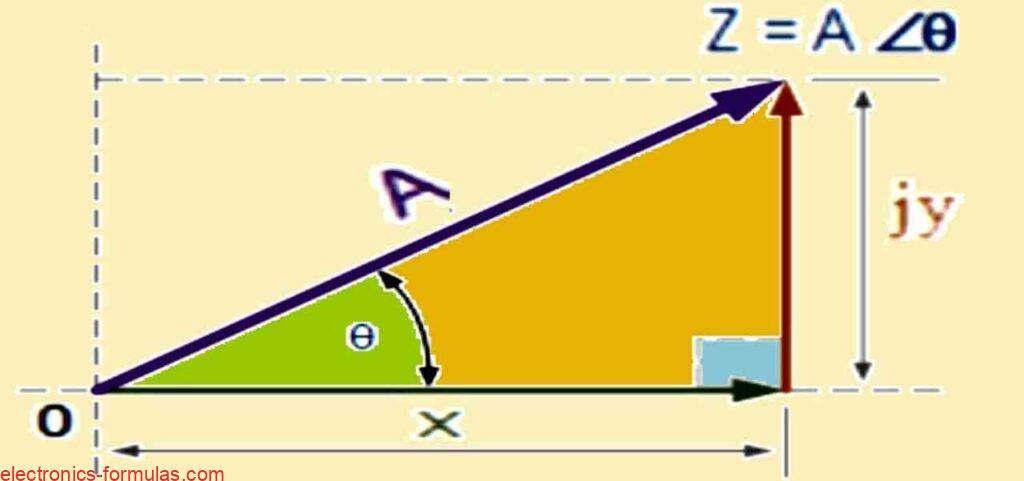
How Polar Form is Based on Triangle and Trigonometry
So we already saw that this triangular form is like the base or foundation for how we show complex numbers in polar format. That means when we want to find the magnitude and the angle of any complex number, then we can just use simple trigonometry rules and the good old Pythagoras triangle formula from school days.
Because trigonometry is that thing which helps us understand how the sides and angles of a triangle are connected, we can now write the relationships like this:
A² = x² + y²
So the magnitude A becomes:
A = √(x² + y²)
Also we can get the x and y parts from A like this:
x = A cosθ,
y = A sinθ
How to Find the Angle θ from the Triangle
Now again, using the same trigonometry stuff, we can find the angle θ of vector A by applying:
θ = tan⁻¹ (y ÷ x)
This gives us how much the vector is turning from the real axis.
So now instead of just showing the complex number as a point (x + jy), in polar form we are showing it as length A and angle θ.
Polar Form Conjugate is Same Length, Opposite Angle
Another thing in polar form, the conjugate of any complex number also follows same trick.
That means the length or magnitude A stays same but the angle θ becomes negative. Simple!
Like if we have a complex number written as:
6 ∠30°,
then its conjugate will be:
6 ∠–30°
So only the direction of rotation flips, but the distance from center (modulus) remains exactly same.
How We Convert Between Polar Form and Rectangular Form
Now we come to the conversion part.
We know that in rectangular form, we show complex numbers by their horizontal and vertical coordinates, the horizontal axis is the real part and the vertical axis is the imaginary part or j-part.
But in polar form, instead of these coordinates, we use the vector’s magnitude A and its angle θ. So both are same thing, just two different styles of showing.
Now using our same example as before, we can explain how to convert back and forth between polar form and rectangular form without getting confused.
Calculations Showing Polar Form into Rectangular Form Conversion (P→R)
- 6∠30o = x + jy
- But we know that x = A.cosθ and y = A.sinθ
- Hence, we have:
- 6∠30° = (6cosθ) + j(6sineθ) = (6cos30°) + j(6sin30°) = (6 x 0.866) + j(6 x 0.5) = 5.2 + j3
Calculations Showing Rectangular Form to Polar Form Conversion (R→P)
(5.2+ j3) = A∠θ
where: A = √5.22 + 32 = 6 and 0 = tan-1 (3/5.2) = 30° Therefore, (5.2 + j3) = 6∠30°
How to Multiply and Divide using Polar Form
So when we want to multiply or divide any complex numbers, that time it becomes much more easier and smarter to use the polar form instead of the rectangular form.
Because in polar form, we do not have to worry about all those x and y coordinates or breaking down real and imaginary parts. Instead, we just focus on the magnitude and the angle.
How to Multiply Two Complex Numbers in Polar Form
Now if we want to multiply two complex numbers in polar format then we just need to do two things step by step:
Multiply the magnitudes of both vectors.
Add their angles together.
That means if we have two complex numbers like:
Z₁ = A₁ ∠θ₁
Z₂ = A₂ ∠θ₂
Then their product will be:
Z₁ × Z₂ = A₁ × A₂ ∠(θ₁ + θ₂)
So easy, Just multiply the lengths and add the angles. No mess!
Rectangular Form is Better for Addition and Subtraction
But now again, when we talk about adding or subtracting complex numbers then it is better to use the rectangular form.
Because in that case, we can just add or subtract real parts and imaginary parts separately like simple math. No angle business here.
So the polar form is like hero for multiplying and dividing but rectangular form is the boss for addition and subtraction.
Z1 x Z2 = A1 x A2 = ∠θ1 + θ2
If we multiply 6 ∠30o and 8 ∠– 45o with each other in polar form we get the following results.
Z1 x Z2 = 6 x 8∠30° + (-45°) = 48∠-15°
Calculations Showing How to Divide in Polar Form
Z1/Z2 = (A1/A2) ∠θ1 + θ2
Z1/Z2 = (6/8) ∠30o – (-45°) = 0.75 ∠75°
Modern scientific calculators come equipped with built-in mathematical functions, facilitating seamless conversion between rectangular (R → P) and polar (P → R) forms.
Expressing Complex Numbers with Exponential Form
So here we are going to see one very famous and super important identity in complex numbers and electrical engineering which is called Euler’s Identity.
It is shown like this:
Z = A × e^(jΦ)
Now according to the Euler’s formula, we can expand this thing like:
Z = A × (cosΦ + j × sinΦ)
That means that any complex number in polar form which is shown with magnitude A and angle Φ, can also be written using exponential format with “e to the power jΦ”.
So now this thing is not just some math formula but it is actually linked with the rotating phasor in the complex plane.
Because when we rotate a phasor vector in anticlockwise direction then its path creates a circular motion and that circular motion is captured by this Euler’s formula.
That is why when we look at the rotating phasor diagram in the complex s-plane or Argand diagram then we can visually understand how this Euler’s identity works.
So this is the idea behind how:
Z = AejΦ = A(cosΦ + jsinΦ)
is used to explain vector rotation in the phasor form.

this Euler’s identity actually looks very much same like the polar form of complex numbers. It clearly shows that when we write any number like A × e^jθ and if its magnitude is 1, then still it is a valid complex number.
This identity is super useful because it helps us to easily convert any complex number from exponential form to polar form.
For example:
2 × e^j30 becomes 2∠30
10 × e^j120 becomes 10∠120
-6 × e^j90 becomes -6∠90
So this same Euler thing also helps us to convert exponential form into rectangular form, using cosine and sine. That means we can go back and forth between all three forms very easily.
Because of this we now get a complete link between:
- Exponential Form
- Polar Form
- Rectangular Form
All three are now connected and we can show any complex number in all of them like this:
Z = x + j × y = A ∠ θ = A × (cosΦ + j × sinΦ)
So this is how Euler’s identity becomes the bridge between these different ways of showing complex numbers and makes our life super easy in electrical engineering and mathematics.
Leave a Reply