A 3-Phase electricity is basically a method we use to create and send electric power over really long distances so that our offices and industries can use it. In this setup we deal with three-phase voltages and currents which we can adjust either increase or decrease, using three-phase transformers. These transformers are pretty cool because they have windings that can be connected in different ways depending on what we need.
Up until now we have been focusing on the simpler single-phase two-winding voltage transformer. This type of transformer is handy because it allows us to change its secondary voltage in relation to the primary supply voltage. But here is where it gets interesting, we can also make voltage transformers that connect not just to one single phase but to two phases, three phases, six phases, and even some really complex setups that can go up to 24 phases especially for those DC rectification transformers.
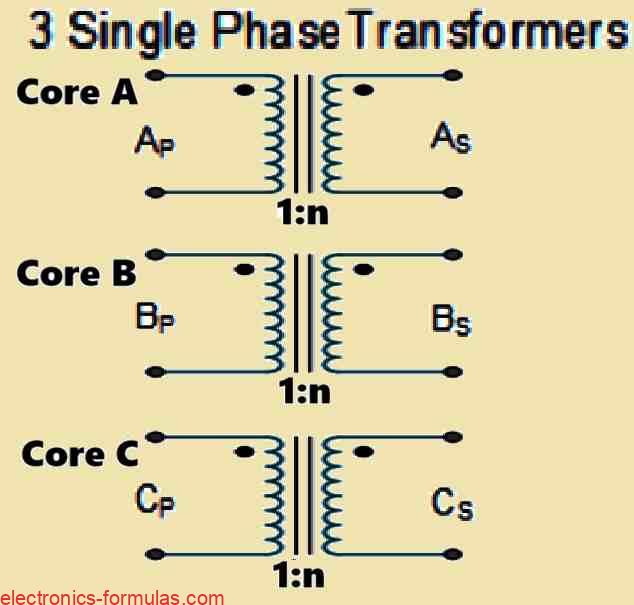
Now if you take three separate single-phase transformers and hook up their primary windings together as well as their secondary windings in a specific way, you can actually use those transformers with a three-phase power supply.
When we talk about three-phase power, which you might see written as 3-phase or even 3φ, we are referring to a system used for generating, transmitting, and distributing electrical power. It is also widely used in all sorts of industrial applications.
The nice thing about three-phase supplies is that they come with a bunch of electrical benefits compared to single-phase power. When we consider three-phase transformers we have to keep in mind that we are dealing with three alternating voltages and currents that are out of sync with each other by 120 degrees in terms of phase time.
Understanding Three Phase Voltages and Currents
It is not possible for a transformer to function as a one-phase to three-phase or three-phase to single-phase phase changer. In order for the transformer connections to work with three-phase supply we must link them collectively in a certain manner to create a three-phase transformer topology.
It is possible to build a three-phase transformer also known as a 3φ transformer by joining three single-phase transformers to create a referred to as three-phase transformer bank or simply by applying an already assembled, balanced three-phase transformer that is made up from three pairs of single-phase windings secured over an individual laminated core.
Given that the copper and iron core are applied with greater effectiveness, a single three-phase transformer is going to be smaller, more lightweight, and less expensive to manufacture compared to three separate single-phase transformers coupled together for the same kVA rating.
Whether utilizing a single three-phase transformer or three independent single-phase transformers, the techniques for combining the primary and the secondary windings remain exactly the same. Let us analyze the configuration shown below:
Analyzing Three Phase Transformer Configurations
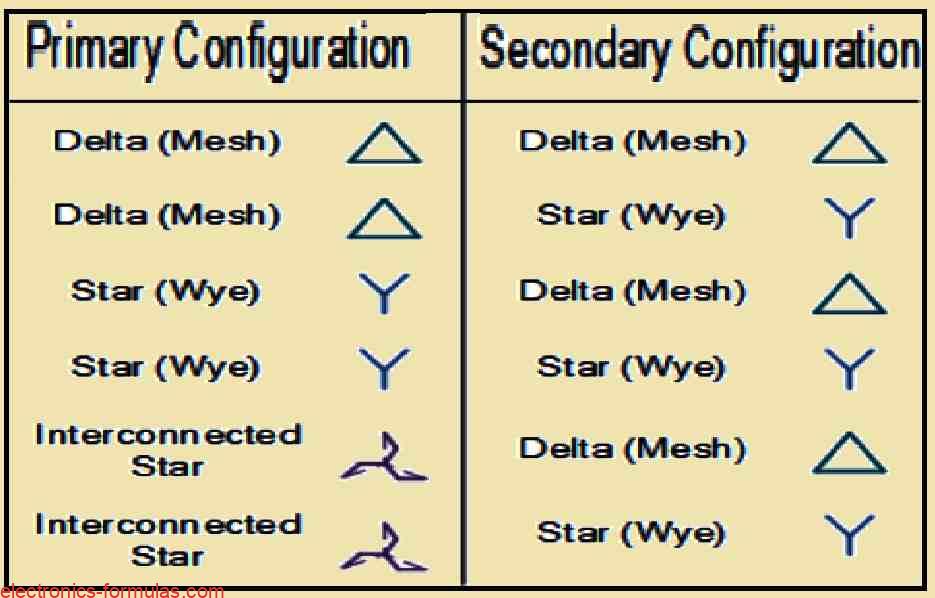
A transformer’s the primary and secondary windings may be linked in a variety of ways as demonstrated, to satisfy almost any need. Three types of connections may be made using three phase transformer windings: “interconnected-star” (zigzag), “delta” (mesh), and “star” (wye).
Depending on the transformer’s intended usage, the three winding arrangements might be the primary delta-connected and secondary star-connected, star-delta, star-star, or delta-delta. In general a transformer is called a polyphase transformer when it is configured for delivering three or more phases.
Understanding Three Phase Transformer Star and Delta Configurations
In addition to selecting on the kind of electrical connections utilized on the primary and secondary sides, the three possible voltages, each of which is 120 electrical degrees apart from the others, also dictate how the transformer’s current flow.
When three single-phase transformers are linked, there is a 120 time-degree phase difference between the magnetic fluxes in the three transformers. Three magnetic fluxes with 120-degree time-phase differences exist in the core of each three-phase transformers.
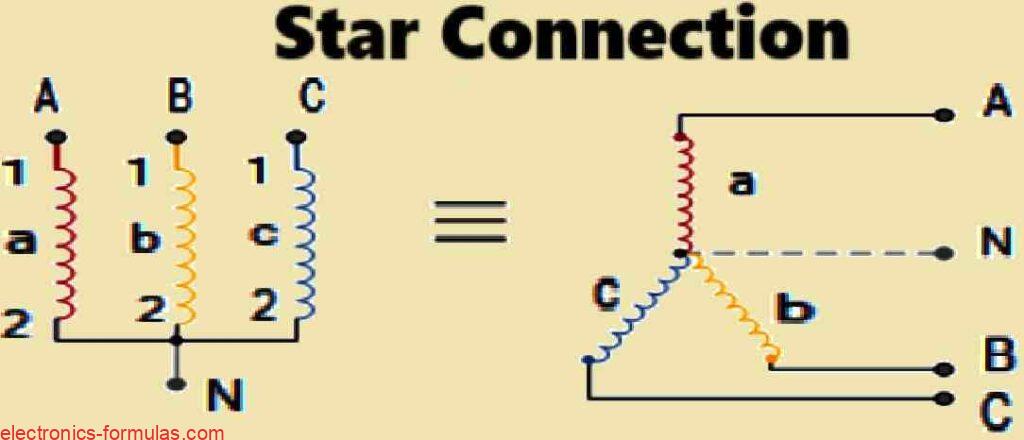
The three primary windings of a three-phase transformer are often marked with the capitalized (upper case) alphabets A, B, and C, which symbolize for the three respective phases of RED, YELLOW, and BLUE.
The three small (lower case) characters a, b, and c are used to identify the secondary windings.
For example the second winding of the primary would have ends that are designated B1 and B2, and the third winding of the secondary would have ends which are labelled c1 and c2 as indicated. This is because each winding includes two ends which are typically marked 1 and 2.
Understanding the Star and Delta Transformer Configurations
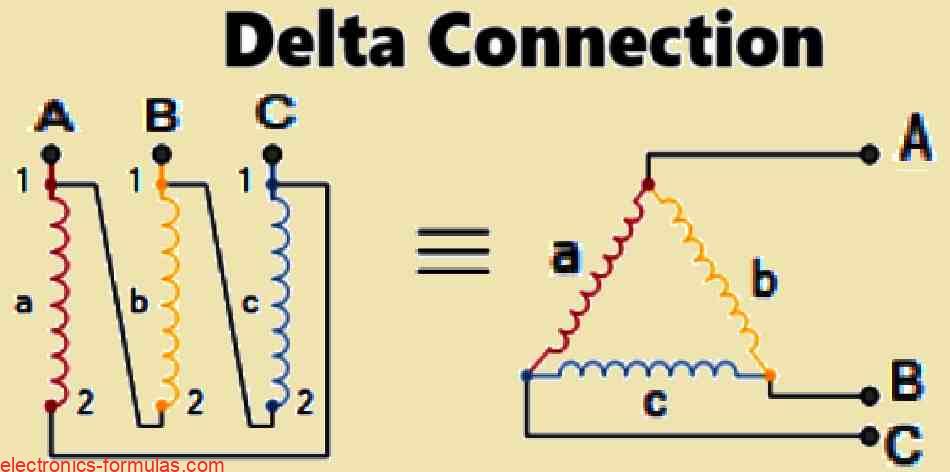
On a three-phase transformer, icons are often used to denote what kind or forms of interconnections are used. In addition to lower case y, d, and z for their respective secondaries, we will also find upper case Y for star connected, D for delta connected, and Z for linked star primary windings.
For the identically wired transformers, we would then designate interconnected star to interconnected star as Zz, Delta to Delta as Dd, and Star to Star as Yy.
Using a Table to Understand 3 Phase Transformer Winding
| Connection | Primary Winding | Secondary Winding |
| Delta | D | d |
| Star | Y | y |
| Interconnected | Z | z |
So we have four possible configurations for connecting three single-phase transformers between their primary and secondary three-phase circuits, as we now know. Delta-Delta (Dd), Star-Star (Yy), Star-Delta (Yd), and Delta-Star (Dy) are the four common combinations.
In comparison to delta transformers, high voltage transformers using star connections have the advantage of decreasing the voltage on a single transformer through fewer number of turns and larger conductors, and therefore making it simpler and less expensive to provide insulation for the coil windings.
However the delta-delta combination includes a significant advantage when compared to the star-delta arrangement: in the event that one of the three transformers in the group malfunctions or is dysfunctional, then the other two will keep operating to provide three-phase power with a capacity equivalent to roughly two-thirds of the transformer’s initial output.
Understanding the Delta-Delta 3-Phase Transformer Configuration

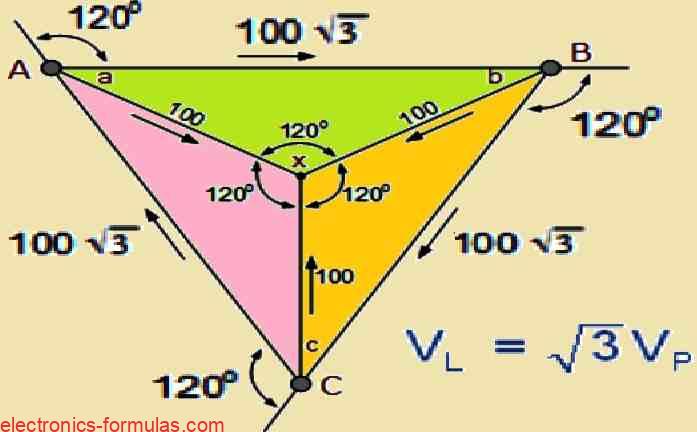
The line voltage (VL) in a delta linked (Dd) set of transformers is exactly the same as the supply voltage (VL = VS). For each phase winding, however, the current is expressed as being 1/√3 × IL of the line current, whereby IL corresponds to the line current.
The requirement that every single transformer must have a winding for the full-line voltage (in our case over 100V) and for 57.7% line current seems a drawback of delta-connected three-phase transformers.
Compared to the star connection, a bigger and more costly coil is required due to the winding’s higher number of turns and the insulation between turns. The absence of a “neutral” or common connection is an additional drawback of delta-connected three-phase transformers.
Every single transformer in the star-star (Yy) or wye-wye configuration comprises one terminal attached to a neutral point or common junction, while the three subsequent terminals of the primary windings are linked to the three-phase mains supply. In any a star connection, the transformer winding needs 57.7% of the turns needed for a delta connection.
A total of three transformers are needed for the star connection, and in the event one of them fails or is disabled, all of the others can also get deactivated. However in electrical power distribution systems, the star-connected three-phase transformer is particularly efficient and cost-effective because, as illustrated, a fourth wire could potentially be attached to work like a neutral point (n) for the three star-connected secondaries.
Understanding the Star-Star 3-Phase Transformer Configuration
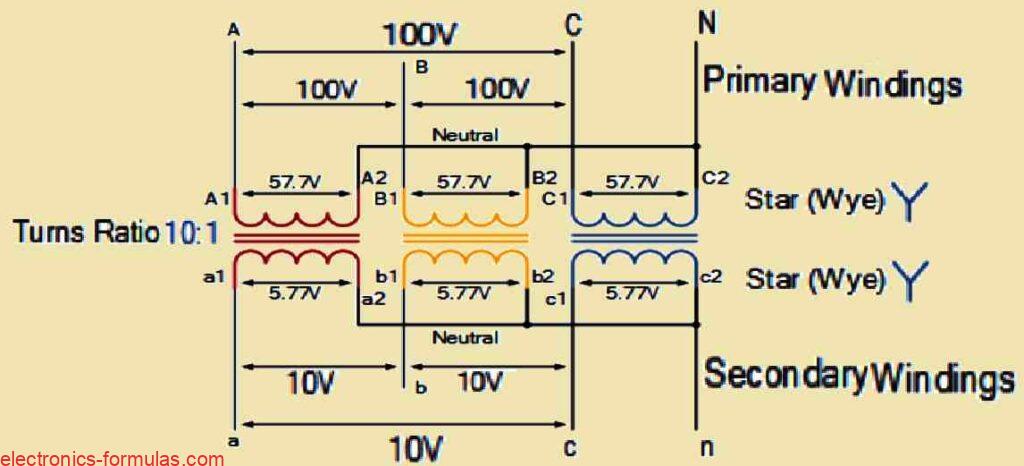
The “line voltage,” or VL, is the voltage between any two lines in a three-phase transformer, while the “phase voltage,” or VP, is the value between any two lines and the neutral point of a transformer that is connected to a star. This phase voltage is equal to 1/√3 × VL of the line voltage between the neutral point and any line connection. Then the primary side phase voltage in the above figure VP, can then be calculated as:
VP = (1/√3) * VL = (1/√3) * 100 = 57.7 Volts
If the line current of the electricity source and the secondary current in each phase of a star-connected set of transformers are equal, in that case IL = IS.
In a three-phase electrical supply, the connection between line and phase voltages and currents could therefore be concluded up as follows:
Table to Sum up the Three-phase Voltage and Current
| Connection | Phase Voltage | Line Voltage | Phase Current | Line Current |
| Star | VP = VL ÷ √3 | VL = √3 * VP | IP = IL | IL = IP |
| Delta | VP = VL | VL = VP | IP = IL ÷ √3 | IL = √3 * IP |
Again this time from the main or secondary side, VP represents the phase-to-neutral voltage whereas VL indicates the line-to-line voltage.
Three phase transformers can also be wired up in the following ways: delta-star Dy, which incorporates a delta-connected primary and a star-connected secondary, or star-delta Yd, in which the primary winding would be star-connected and the secondary being delta-connected.
With the main windings supplying the utility company with a three-wire balanced load and the secondary windings supplying the necessary fourth-wire neutral or ground connection, delta-star linked transformers are frequently utilized in low power distribution.
The transformer’s total turns ratio gets more complex when the primary and secondary have independent winding connections, such as star or delta. There is a chance that a three-phase transformer with a 1:1 turns ratio will be connected as delta-delta (Dd) or star-star (Yy). In other words, the windings’ input and output voltages are equal.
For low power distribution, delta-star connected transformers are frequently utilized. The electricity distribution corporation receives a three-wire balanced load from the primary windings whereas the secondary windings deliver the necessary fourth-wire neutral or earth connection.
This complicates the transformer’s total turns ratio because the primary and secondary include independent winding connections, such as star or delta. A three-phase transformer could come with a 1:1 turns ratio if it has been connected as delta-delta (Dd) or star-star (Yy). This means that the windings’ input and output voltages happen to be equal.
On the other hand, every single star-connected main winding is going to get the supply’s phase voltage VP, that is approximately 1/√3 × VL, whenever the 3-phase transformer is connected in star–delta, (Yd).
Considering these windings have been delta-connected, the voltage 1/√3 × VL will subsequently turn into the secondary line voltage once the same voltage is generated in each matching secondary winding.
A star-delta connected transformer would consequently produce a √3:1 step-down line-voltage ratio with a 1:1 turns ratio.
The turns ratio calculation for a transformer with a star-delta (Yd) connection thus turns into:
Formula for Star-Delta Turns Ratio
TR = NP/NS = VP/(√3 * VS)
Similarly a transformer connected to a delta-star (Dy) with a 1:1 turns ratio will increase the line-voltage ratio by a factor of 1:√3. As a result, the turns ratio for a transformer with a delta-star connection will be:
Formula for Delta-Star Turns Ratio
TR = NP/NS = (√3 * VP)/VS
Table Indicating Three-phase Transformer Line Voltage and Current
We could subsequently describe the secondary voltages and currents of the transformer for each of the four fundamental three-phase transformer topologies with regards to the primary line voltage VL and its primary line current IL, as shown in the table below.
| Primary-Secondary Configuration | Line Voltage, Primary or Secondary | Line Current, Primary or Secondary |
|---|---|---|
| Delta-Delta | VL → n * VL | IL → IL / n |
| Delta-Star | VL → √(3) * n * VL | IL → IL / (√(3) * n) |
| Star-Delta | VL → (n * VL) / √(3) | IL → (√(3) * IL) / n |
| Star-Star | VL → n * VL | IL → IL / n |
In the above table, VL represents the line-to-line voltage and VP indicates the phase-to-neutral voltage, and n denotes the transformer’s “turns ratio” (T.R.) of the number of secondary windings (NS) divided by the amount of primary windings: (NP) * (NS/NP).
Solving a 3-Phase Transformer Problem #1
A 110 volt 60Hz three-phase supply powers the primary winding of a delta-star (Dy) connected 60VA transformer. Calculate the secondary side voltages and currents assuming the transformer’s primary winding contains 600 turns and its secondary winding comprises 120 turns.
Given:
- Primary voltage (VL(primary)) = 110 V
- Frequency = 60 Hz
- Transformer power = 60 VA
- Primary turns (Np) = 600
- Secondary turns (Ns) = 120
- Configuration = Delta-Star (Dy)
- Determine the turns ratio:
- n = Ns / Np
- n = 120 / 600
- n = 0.2
- Calculate the secondary line-to-line (line) voltage:
For a delta-star configuration, the secondary line voltage is:
VL(secondary) = √(3) * n * VL(primary)
Let’s Substitute the values:
VL(secondary) = √(3) * 0.2 * 110 VL(secondary) ≈ 38.1 V
- Calculate the secondary phase voltage:
In a star connection, the phase voltage is related to the line voltage by:
Vph(secondary) = VL(secondary) / √(3)
Let’s Substitute the values:
Vph(secondary) = 38.1 / √(3) Vph(secondary) ≈ 22.0 V
- Calculate the secondary phase current:
The phase current is derived from the transformer power and phase voltage:
Iph(secondary) = Power / (3 * Vph(secondary))
Substitute the values:
Iph(secondary) = 60 / (3 * 22.0)
Iph(secondary) ≈ 0.91 A
- Calculate the secondary line current:
In a star connection, the line current will be equal to the phase current:
IL(secondary) = Iph(secondary)
So, IL(secondary) ≈ 0.91 A
Final Answers:
- Secondary Line Voltage (VL(secondary)) ≈ 38.1 V
- Secondary Phase Voltage (Vph(secondary)) ≈ 22.0 V
- Secondary Line Current (IL(secondary)) ≈ 0.91 A
- Secondary Phase Current (Iph(secondary)) ≈ 0.91 A
Understanding Three Phase Transformer Construction
As was already mentioned, a three-phase transformer is basically three single-phase transformers connected across each other over a common laminated core.
If we merge the three windings upon a single magnetic circuit, as demonstrated, then it is possible to save significant cost, space, and weight.
The three magnetic circuits that are typically interlinked in a three-phase transformer provide an even spread of the dielectric flux between the high and low voltage windings.
A transformer with a three-phase casing can be an exception to this requirement. Despite being connected, the three cores of the shell form of structure are not interconnected.
Internal Construction of a Standard Three Phase Transformer
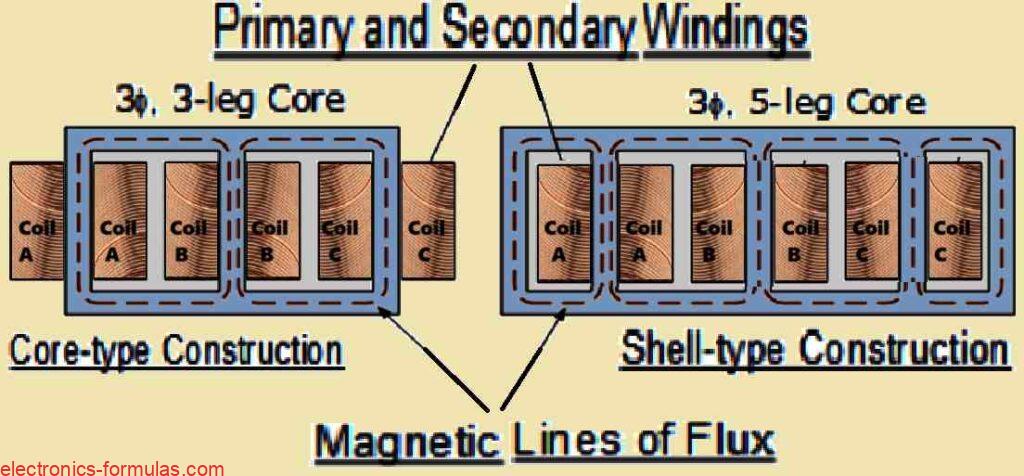
The widely used design approach for three-phase transformers that facilitates magnetic coupling of the phases is the three-limb core-type construction.
Through the three magnetic fluxes in the core, produced by the line voltages which varies in time-phase by 120 degrees, the flux from each limb utilizes the remaining two limbs for its return path. As a result, a sinusoidal secondary supply voltage is produced by the flux in the core, sticking to almost a sinusoidal waveform.
Compared to the core-type, the shell-type core with five-limb type three-phase transformer architecture is greater in weight and more costly to create.
Since five-limb cores may be produced with less height, these usually serve the purpose for extremely massive power transformers. The core components, electromagnetic windings, metal housing, and conditioning of a shell-type transformer are largely identical to those of the bigger single-phase models.
References:
Leave a Reply