We know that the Butterworth filter is a useful tool for electronics professionals but there is a trade-off with its performance. It is superior to other filter types in that it produces a completely flat response in the passband and stopband, but this ideal characteristic comes at the price of a wider transition band.
This transition band is essential for applications that need exact control over frequency. It depicts the frequency range at which the filter’s output switches from allowing signals (passband) to blocking them (stopband). A small transition band can be crucial for our applications such as control loops and communication systems in order to reduce signal distortion and guarantee system stability.
Now, we are aware that the total number of reactive parts (capacitors or inductors) a filter uses directly affects its complexity, or order. The roll-off rate of the filter which controls how abruptly the passband transitions into the stopband, is greatly influenced by this sequence.
Also, the typical roll-off of a first-order filter is 20 dB per decade or 6 dB per octave. This means that for every tenfold increase in frequency, the filter’s output attenuates by 20 dB.
We can create high-order filters, like third, fourth, and fifth-order designs, simply by cascading first and second-order filter stages. For example, by hooking up two second-order low-pass filters in series, we might be able to produce a fourth-order low-pass filter. Although cascading can theoretically produce any desired filter order, there are real-world limitations. Increasing the filter order results in larger, more expensive circuits with potentially worse accuracy.
Understanding Decades and Octaves in Frequency Scaling
Now, I would want to explain on the concept of Decades and Octaves in relation to frequency scaling which is critical for any electronic engineer dealing with amplifiers and filters.
On the frequency scale, a decade indicates a tenfold increase or decrease in frequency. This means that in order to change frequencies within the same decade, we would need to either multiply or divide the initial frequency by ten. For example, the range from 2 Hz to 20 Hz comprises a decade. If we broaden on this example, the range from 50 Hz to 5000 Hz covers two decades: first from 50 Hz to 500 Hz, then from 500 Hz to 5000 Hz.
An Octave, on the other hand, involves the frequency being doubled or halved. Specifically, doubling the frequency moves us up by one octave, halving it moves us down by one octave. As an example one octave is defined as the frequency range of 10 Hz to 20 Hz. To illustrate, the frequency range from 2 Hz to 16 Hz is divided into three octaves: 2 Hz to 4 Hz (one octave), 4 Hz to 8 Hz (another octave), and 8 Hz to 16 Hz (a third octave), with each step doubling the frequency.
Learning these concepts can be critical, because logarithmic scales are widely used in the frequency domain to express frequency values, which can be especially important for us when dealing with frequency response in amplifiers and filters.
Logarithmic Frequency Scale
Now I would like to discuss the logarithmic frequency scale and how it relates to filters of different orders in the context of filter design.

When working with filters, all of the frequency-determining resistors and capacitors are similar, therefore greatly simplifies the calculations we perform. The cut-off frequency, or corner frequency (fc), for every filter—whether first, second, third, or fourth-order, is the same. This may be determined through the commonly used formula:
fc = 1 / (2 * π * R * C).
Higher-order filters, such as third and fourth-order high-pass filters, are actually quite simple to implement. We can create these filters simply by moving the positions of the frequency-determining components (resistors and capacitors) in the equivalent low-pass filter arrangement. This concept is compatible with the methods discussed in our previous Low Pass and High Pass filter lessons. But it is worth noting that the total gain of these high-order filters remains fixed, because the frequency-determining components continue to be the same across the different orders of the filter.
Understanding Filter Approximations
In earlier discussions on filter approximations, We looked at first-order low-pass and high-pass filter circuits, as well as their frequency and phase responses. In an ideal case, we would want a filter that provides maximum pass-band gain along with outstanding flatness, minimal stop-band attenuation, and a very rapid transition from pass to stop band. Fulfilling all of these objectives simultaneously is difficult, but it turns out that a variety of network responses could satisfy these criteria.
Considering the complicated nature of linear analog filter construction it is not surprising that numerous “approximation functions” are actually utilized. These functions use mathematical techniques to closely approximate the intended transfer function for a filter design.
Among the most common forms of these approximation functions are Butterworth, Elliptical, Bessel, Chebyshev, and Cauer filters. Among these basic linear analog filter approximations I am going to focus on the Butterworth filter, especially the low-pass Butterworth filter design. This is because the Butterworth filter is the most commonly used among them, offering a fair mix of performance and simplicity in a wide range of practical applications.
Designing a Low Pass Butterworth Filter Circuit
When we want to design a Low Pass Butterworth Filter we consider its characteristic “maximally flat” frequency response. This phrase refers to the filter’s pass band which is designed to keep the frequency response as flat as possible, from 0 Hz (DC) to the cutoff frequency without any ripples. In simple terms, the Butterworth filter is intended to provide a smooth and continuous pass band response up to -3 dB at the cutoff frequency.
Above the cut-off frequency, the response declines to the stop band at a rate of 20 dB per decade or 6 dB per octave. This steady roll-off is due to the filters quality factor, or “Q,” which is fixed at 0.707.
That said, there can be a drawback to using the Butterworth filter. Although it specializes at generating a flat pass band, this is at the expense of having a rather wide transition band.
This implies that the filter makes a more gradual transition from the pass band to the stop band. Furthermore, the Butterworth filter has less desirable phase characteristics compared to other filters. For the purposes of comparison, the ideal frequency response, sometimes known as a “brick wall” filter, and the typical Butterworth approximations for different filter orders are shown below.
What is the Ideal Frequency Response for a Butterworth Filter?
Whenever we are dealing with Butterworth filters, it is important to remember that increasing the filter order requires additional cascaded stages in the design. This means that the filter’s response is approaching the ideal “brick wall” characteristic, and this denotes an ideal filter with a sudden shift from the pass band to stop band.
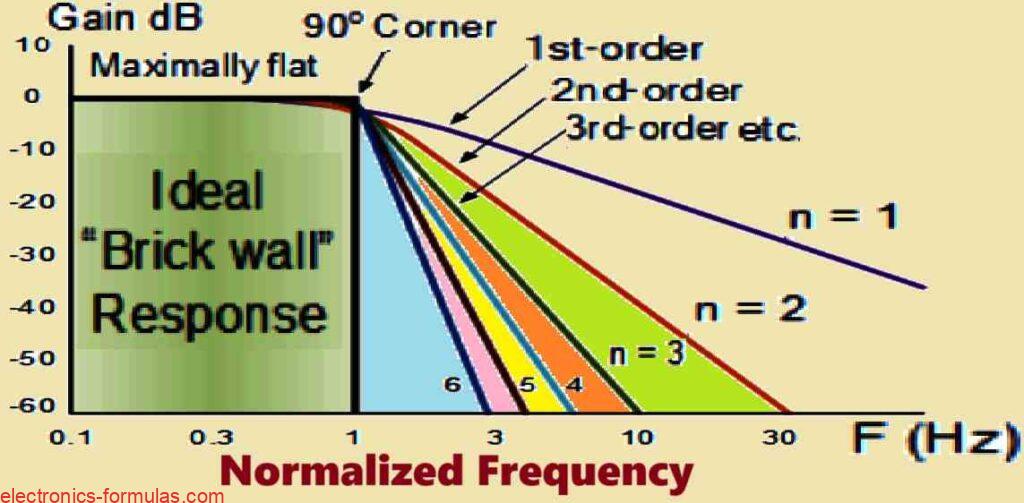
In reality, however, obtaining Butterworth’s optimum frequency response is difficult for us because it might create excessive passband ripple.
The frequency response of a “nth” Order Butterworth filter is represented by the following generalized equation:
H(jω) = 1/√[1 + ε2(ω/ωp)2n]
In this equation:
- n denotes the filter order,
- ω = 2πf, where f is the frequency,
- ε is the maximum pass band gain, denoted as (Amax).
When Amax is specified with a cut-off -3dB corner point (fc), ε will be equal to one, meaning that ε2 is likewise one. If the objective is to determine Amax at a different voltage gain value, such as 1dB or 1.1220 (1dB = 20*logAmax), then the new epsilon, ε, is calculated with the help of the equation:
H1 = H0/√(1 + ε2).
Where H0 represents the maximum pass band gain (Amax).
H1 represents the minimum pass band gain.
If we change the order of the equation, we get:
H0/H1 = 1.1220 = √(1 + ε2), finally gives us ε = 0.5088
A filter’s Frequency Response may be mathematically characterized using the standard Voltage Transfer Function H(jω), which is expressed as:
H(jω) = Vout(jω)/Vin(jω)
- In this equation:
- Vout indicates the output signal voltage.
- Vin indicates the input signal voltage.
- j is equal to the square root of -1 (√-1)
- ω denotes the radian frequency (2πƒ)
Please remember that we can also write the expression ( jω ) as ( s ) which then indicates the S-domain, which is also the resultant transfer function for a second-order low pass filter. We can express the above with the following equation:
H(s) = Vout/Vin = 1/(S2 + S + 1)
Normalized Polynomials for Low-Pass Butterworth Filters
Thanks to Butterworth who has developed standard tables of normalized second-order low-pass polynomials to help us design low-pass filters. In these tables we can find the coefficient values that are equivalent to a cut-off or the corner frequency of one radian per second.
| n | Normalized Denominator Polynomials in Their Factored Form |
| 1 | (1+s) |
| 2 | (1+1.414s+s2) |
| 3 | (1+s)(1+s+s2) |
| 4 | (1+0.765s+s2)(1+1.848s+s2) |
| 5 | (1+s)(1+0.618s+s2)(1+1.618s+s2) |
| 6 | (1+0.518s+s2)(1+1.414s+s2)(1+1.932s+s2) |
| 7 | (1+s)(1+0.445s+s2)(1+1.247s+s2)(1+1.802s+s2) |
| 8 | (1+0.390s+s2)(1+1.111s+s2)(1+1.663s+s2)(1+1.962s+s2) |
| 9 | (1+s)(1+0.347s+s2)(1+s+s2)(1+1.532s+s2)(1+1.879s+s2) |
| 10 | (1+0.313s+s2)(1+0.908s+s2)(1+1.414s+s2)(1+1.782s+s2)(1+1.975s+s2) |
Calculating Designing a Butterworth Low Pass Filter Circuit
Let us assume the following parameters for an active low pass Butterworth filter: Amin = -20dB at the stop band frequency (ωs) of 800 radian/sec, and Amax = 0.5dB at the pass band frequency (ωp) of 200 radian/sec (31.8Hz). Using the above data we want to create a Butterworth filter circuit that satisfies these specifications .
In the beginning please understand that the highest pass band gain, Amax = 0.5dB, equals a gain of 1.0593. Also, keep in mind that, with a frequency (ωp) of 200 rads/s, we will have 0.5dB = 20log(A). Using this information, the value of epsilon ε may be calculated as follows:
1.0593 = √(1 + ε2),
∴ ε = 0.3495, where ε2 = 0.1221.
Next, at a stop band frequency (ωs) of 800 rads/s, or 127.3 Hz, the minimum stop band gain Amin will be equal to -20dB, which translates to a gain of 10 [-20dB = 20*log(A)].
When we substitute the above values into our earlier generalized equation for a Butterworth filters, we get the frequency response as explained below:
H(jω) = H0/√[1 + ε2(ω/ωp)2n]
1/10 = 1/√[1 + 0.1221(800/200)2n]
(10)2 = 1 + 0.1221(800/200)2n
∴ 100 – 1 = 0.1221 * 42n
42n = 99/0.1221 = 810.811
4n = √810.811 = 28.475
∴ n = log 28.475/log4
= 2.42
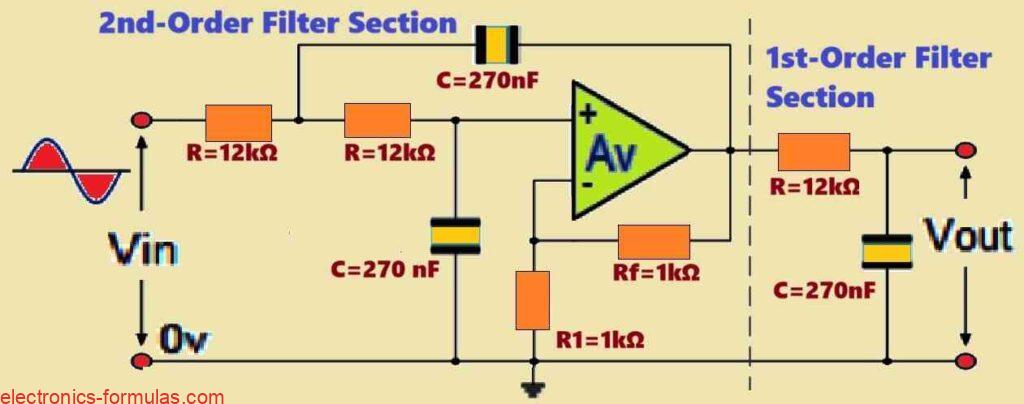
Given that (n) must be an integer, the smallest integer greater than 2.42 is (n = 3). This means that now we need a third-order filter. Therefore, to achieve a third-order Butterworth filter we will need to combine a second-order filter stage with a first-order filter stage in a series.
If we refer to our above normalized low-pass Butterworth polynomials table, the coefficients for a third-order filter are expressed as [(1 + s)(1 + s + s2)]. From this setup we get a gain of (3 – A = 1), which implies that (A = 2). Using the relationship A = 1 + (Rf/R1), we can select both the feedback resistor (Rf) and the resistor (R1) to be 1kΩ. This choice satisfies the equation [(1kΩ/1kΩ) + 1 = 2].
Although we are aware that the 1/CR method may be employed to identify the cut-off corner frequency, or the -3dB point (ωo), we must first determine ωo from the pass band frequency, or ωp, therefore:
H(jω) = H0/√[1 + ε2(ωo/ωp)2n]
3dB = 1.414 @ ω = ωo
1/1.414 = 1/√[1 + ε2(ωo/ωp)2n]
2 = 1 + ε2(ωo/ωp)2n
∴ 1 = ε(ωo/ωp)n
ωon = ωpn/ε
ωo3 = 2003/0.3495
ωo3 = 22.889 * 106
ωo = 283.93 which almost equal to 284 rads/s
Thus the cut-off corner frequency that we obtained above is 284 rads/s, or 45.2Hz, (284/2π). We can now subsequently obtain the resistor and capacitor values for our third-order circuit using our well-known formula 1/CR.
284 rads/s = 1/CR, let us use 12 kΩ for R.
∴ The Capacitor C = 1/(284 * 12000) = 0.29 µF, The nearest E12 series being: 0.27 µF (270 nF) or 0.33 µF (330 nF)
Understanding Third-order Butterworth Low Pass Filter Circuit
Hence, for our 3rd-order Butterworth Low Pass Filter circuit with a corner frequency of 45.2Hz, we can select C as 270 nF and R = 12 kΩ
Lastly, the design of our circuit for the third-order low pass Butterworth filter is as simple as outlined below: it has a cut-off corner frequency of 284 rads/s, or 45.2 Hz, a maximum pass band gain of 0.5 dB, and a minimum stop band gain of 20 dB.
References: Butterworth filter
What is wrong with this butterworth filter, how can it be improved?
Leave a Reply