In a passive RC integrator circuit, we see that the input is actually connected to a resistor, while the output voltage is measured across the capacitor.
This setup is basically the complete opposite of what goes on in an RC differentiator circuit.
In RC integrator, when we make input signal high, the capacitor then starts charging up and when we make the input signal low, the capacitor begins to discharge.
Now when it comes to electronics, this basic series connection of a resistor and a capacitor, commonly referred to as an RC circuit, has a lot of different uses and applications.
You might find this type of RC designs in almost everything, from simple charging and discharging circuits all the way up to more complex high-order filter circuits.
The design might look like a pretty straightforward two-component passive circuit, but the behavior of this basic RC circuit can vary quite a bit, depending on both the type of input signal you apply and the frequency of that signal.
So when we talk about a passive RC network, we find that it is just a resistor placed in series with a capacitor. That’s it—just a fixed resistance paired up with a capacitor.
But here’s the thing: the capacitor in this setup has something called frequency-dependent reactance which basically means that the way it reacts to changes depending on the frequency of the signal applied to it.
As we increase the frequency across the capacitor plates, its reactance decreases.
At lower frequencies, the capacitor’s reactance, which we call XC, is actually quite high. But as the frequency gets higher, the reactance becomes much lower.
This all happens due to the standard capacitive reactance formula which is XC = 1/(2πfC). You might remember seeing this effect when we talked about passive low-pass filters in our earlier tutorial.
When we feed an RC integrator with a sine wave as the input signal, what we find is that it behaves just like a basic low pass filter (LPF) once we go above its cut-off point.
This cut-off, or corner frequency, is directly tied to the RC time constant, which we call tau (τ), of the series network.
So when we apply a pure sine wave through it, the RC integrator functions as a passive low pass filter, reducing the output once we go past the cut-off frequency point.
As we have seen before, the RC time constant shows us how the resistance and capacitance are related over time.
This gives us a clear idea regarding how these components interact, with time being measured in seconds and being directly proportional to both the resistance R and the capacitance C.
So what we are really talking about here is that the rate at which the capacitor charges or discharges depends on this RC time constant τ, which is simply the RC.
Let us take a look at the circuit below to investigate this idea further.
Evaluating a Passive RC Integrator Circuit
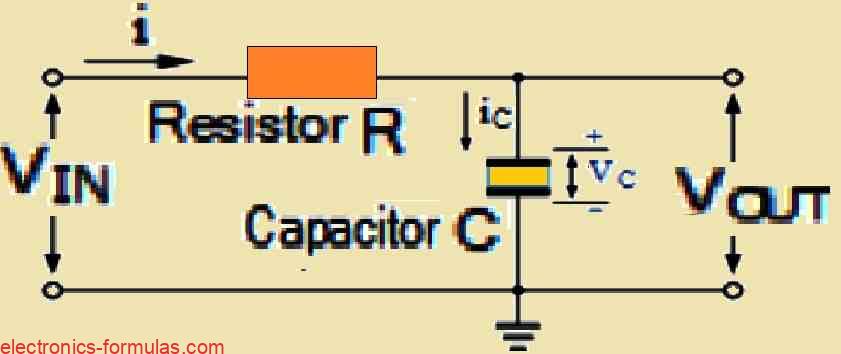
In an RC integrator circuit, we directly apply the input signal to the resistor and then we take the output across the capacitor.
In this setup, the VOUT is the same as the voltage across the capacitor VC. Now, since we are working with a capacitor which is a frequency-dependent element, the amount of charge that builds up across its plates is actually equal to the time-domain integral of the current.
In other words, it takes some time for the capacitor to fully charge, because it cannot just charge up instantly—it only charges exponentially over time.
So because of this, we can express the capacitor’s charging current with the following equation:
iC(t) = C(dVC(t)/dt).
This basically tells us that the current flowing through the capacitor is related to how fast the voltage across the capacitor is changing over time, and that change is scaled by the capacitance C.
The basic equation we just derived above, iC = C(dVc/dt) can also be rewritten to show the instantaneous rate of change of charge Q with respect to time.
This gives us the standard equation:
iC = dQ/dt.
In this case the charge Q, is simply the capacitance multiplied by the voltage across the capacitor.
So we get Q = C * VC, which just means capacitance times voltage.
Now when we talk about how quickly the capacitor charges or discharges, we find that the rate is directly proportional to both the resistance and the capacitance in the circuit.
These two factors together gives us what we call the time constant of the circuit.
So in an RC integrator circuit, the time constant is the time interval that equals the product of R (resistance) and C (capacitance).
Because the capacitance is expressed by the term Q/Vc, where Q is the electrical charge and it is the flow of current (i) over a certain amount of time (t)—which is simply the product of i * t, measured in coulombs—and by using Ohm’s law, we know that voltage (V) is equal to i * R, and thus we can plug these values into the equation for the RC time constant to get the final expression, as shown below:
Evaluating the RC Time Constant
RC = R(Q/V)
= R[(i * T)/(i * R)]
∴ RC = T
or T = RC
So when we look at the above equation, we can see that both the current (i) and the resistance (R) end up canceling out each other, which leaves us with just T.
This tells us that the time constant of an RC integrator circuit only has one dimension, and that is time, measured in seconds. We represent this time constant with the Greek letter tau τ.
It is important to note that this time constant tells us how long it takes, in seconds, for the capacitor to either charge up to 63.2% of the maximum voltage or discharge down to 36.8% of that maximum voltage.
Thus, the tau τ gives us a pretty clear idea of the charging and discharging speed of the capacitor in the circuit.
Analyzing the Voltage across the Capacitor
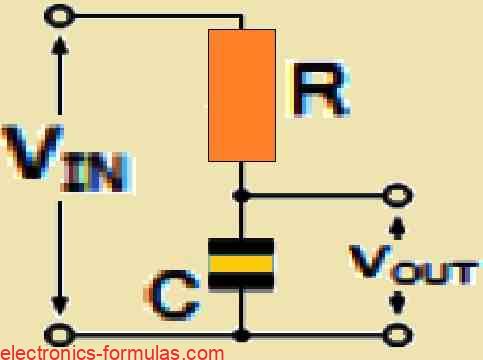
As we mentioned earlier, in an RC integrator circuit, the output voltage is the same as the voltage across the capacitor. Therefore we can say that VOUT is equal to VC.
This voltage is directly proportional to the charge Q, that is being stored on the capacitor and we can express this with the equation:
Q = V x C.
What this means for us is that the output voltage represents the integral of the input voltage and how much integration we get depends on the values of the resistor (R) and the capacitor (C) which together determine the time constant of the network.
We also saw earlier that the current through the capacitor can be written as the rate at which the charge Q is changing over time.
Based on one of the basic rules of differential calculus, the derivative of Q with respect to time is dQ/dt.
Since we know that the current “i” is equal to dQ/dt, we can put that together and get the relationship:
Q = ∫idt (this gives us the charge Q on the capacitor at any given instant of time).
Now, since we connect the input signal to the resistor, the same current “i” has to flow through both the resistor and the capacitor.
That means the current through the resistor (iR) is equal to the current through the capacitor (iC).
This produces a voltage drop across the resistor VR.
So we can express the current flowing through this series RC network through the following equation:
i(t) = VIN/R
= VR/R
= C(dV/dt).
∴ VOUT = VC = Q/C = (∫idt)/C = 1/C(∫i(t)dt)
Now that we know i = VIN/R, we can substitute this into the above equation.
Then after rearranging everything, we can solve for VOUT as a function of time which gives us the final expression:
VOUT = (1/C)∫[(VIN/R)dt]
Understand the RC Integrator Formula
So basically, the output we get from an RC integrator circuit, which is the voltage across the capacitor, is actually equal to the time integral of the input voltage VIN multiplied by a constant of 1/RC. Here, RC is what represents the time constant τ, that we have been talking about.
Now, if we assume that the initial charge on the capacitor is zero, meaning VOUT starts at 0, and we also assume that the input voltage VIN is constant, then we can express the output voltage VOUT at any instant of time, through the following equation in the time domain:
VOUT = 1/RC(∫0t(VIN(t)dt)
From the above data we can say that an RC integrator circuit is essentially a setup where the output voltage VOUT is directly proportional to the integral of the input voltage.
With this information in hand, let us now take a closer look at what happens when we apply a single positive pulse in the form of a step voltage to the RC integrator circuit.
We are going to see how the circuit responds and what changes occur as the pulse moves through the circuit.
Effect of a Single Pulse on an RC Integrator Circuit

When we apply a voltage pulse with a single step to the input of an RC integrator, we notice that the capacitor begins to charge through the resistor in response to this pulse.
But it is important to remember that this output does not happen right away, the voltage across the capacitor does not just change in an instant.
Instead, it increases in an exponential manner as the capacitor charges and the speed of this charging process is defined by what we refer to as the RC time constant which we can express as τ = RC.
At this point it is clear to us that the rate at which the capacitor charges up or discharges down is controlled by this time constant inherent to the circuit.
If we consider a perfectly ideal step voltage pulse input, meaning if we think of both the leading and trailing edges to be instantaneous, then we find that the voltage across the capacitor rises during the charging phase and falls during the discharging phase.
This change occurs exponentially over time, and the rate at which this takes place can be understood through the following equations:
Formula for Charging Capacitor:
VC(t) = V[1 – e-(t/RC)]
Formula for Discharging Capacitor:
VC(t) = V[e-(t/RC)]
Plotting the percentage of charge or discharge of the capacitor for each unique R time constant is therefore possible if we assume that the capacitor voltage is one volt (1V), as the accompanying table below illustrates.
| Time Constant | Capacitor Charging | Capacitor Discharging |
| τ | % Charged | % Discharged |
| 0.5 | 39.4% | 60.6% |
| 0.7 | 50% | 50% |
| 1 | 63.2% | 36.7% |
| 2 | 86.4% | 13.5% |
| 3 | 95.0% | 4.9% |
| 4 | 98.1% | 1.8% |
| 5 | 99.3% | 0.67% |
It is important to note that when we reach 5 time constants or even longer, the capacitor is regarded as being completely and thoroughly charged, or fully discharged.
Solving a Practical RC Integrator Circuit Problem
Now let us imagine that we have an RC integrator circuit, which is made up of a resistor with a value of 10 kΩ and a capacitor with a capacitance of 10 microfarad, as illustrated in the following diagram.
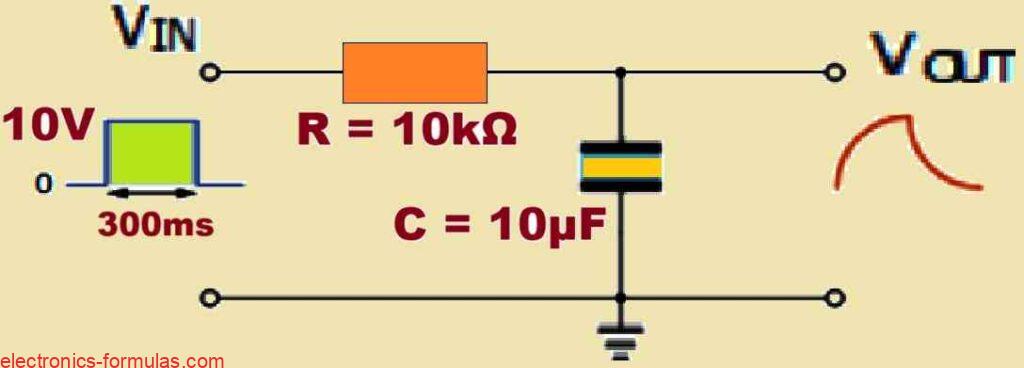
Therefore we can calculate the time constant τ of the RC integrator circuit through the following formula:
RC = 10 kΩ x 10 uF = 100ms.
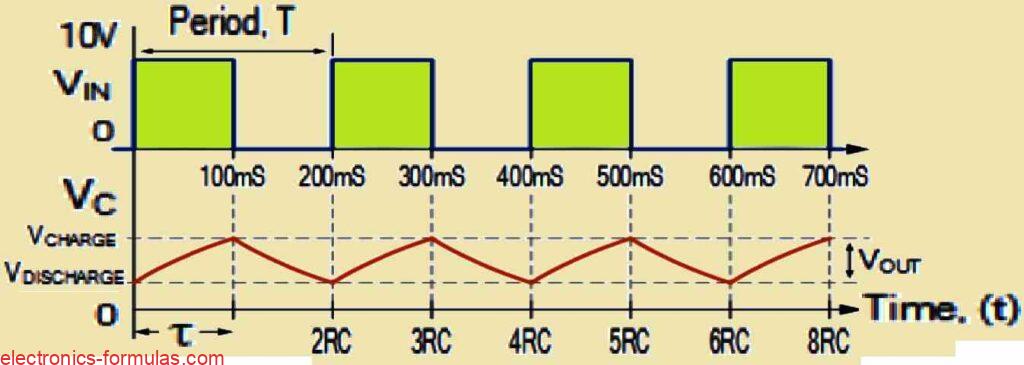
Now If we apply a step voltage pulse to the input of the above RC circuit, let us say it lasts for about 3 time constants which is equivalent to 300 milliseconds, then we can refer to the table above and observe that the capacitor will charge up to approximately 95.0% of its maximum charged value.
If we consider this pulse to have an amplitude of 10 volts, that means we are looking at a voltage of 9.5 volts across the capacitor before it starts to discharge back through the resistor to the source as the input pulse returns to a value of zero.
Now suppose that we allow the capacitor to completely discharge over a period of five time constants, or 500 milliseconds, before the next input pulse arrives, we can refer to the graph below showing us the charging and discharging curves, which would resemble something like this:
Graph Showing RC Integrator Charging/Discharging Curves
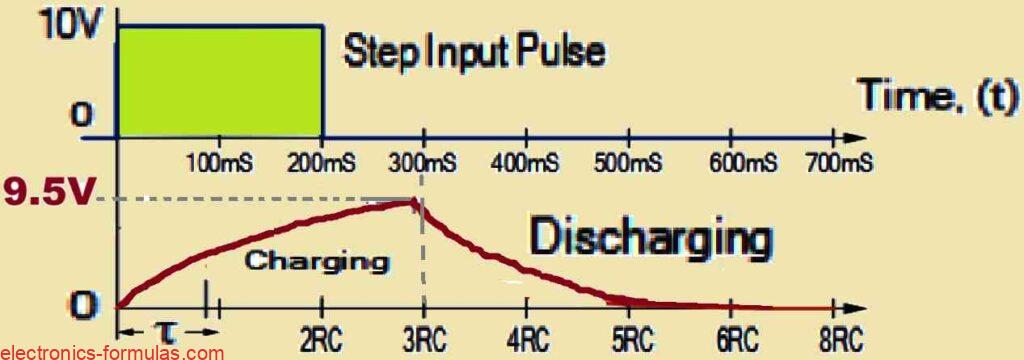
Remember that the capacitor is in the process of discharging from an initial voltage level of 9.5 volts which corresponds to 3 time constants, rather than starting from the 10 volts that we initially applied.
Now we can observe that since the RC time constant remains constant, any changes we make to the width of the input pulse will have an impact on the output produced by our RC integrator circuit.
If we increase the pulse width to a duration that is equal to or even greater than 5 times the RC time constant, we will find that the shape of the output pulse closely resembles to that of our input pulse.
This happens because, in this scenario the output voltage will rise to match the same level as the input voltage.
On the contrary if we reduce the pulse width to less than 5 times the RC time constant, we will see that the capacitor will only be able to charge partially.
In this case it will not reach the maximum input voltage, which results in a smaller output voltage.
This happens because the capacitor simply does not have enough time to charge fully, giving rise to an output voltage that is directly proportional to the integral of whatever input voltage we have applied.
To illustrate this further let us consider a situation where our input pulse is set to one time constant, specifically, 1RC.
In this case, we will notice that instead of charging and discharging between 0 volts and 10 volts as one might initially expect, the capacitor will actually fluctuate between 63.2% and 38.7% of the voltage present across it at the moment of change.
It is important for us to understand that these specific values are governed by our RC time constant.
Effect of Fixed Time Constant for an RC Integrator Circuit
Now, when we consider a continuous pulse input, it becomes clear that there exists a specific relationship between the periodic time of our input signal and the RC time constant of the circuit.
In this scenario, we can expect the integration of the input to occur which results in an output that features a kind of ramp-up followed by a ramp-down effect.
However for our circuit to operate effectively as an integrator, we need to ensure that the value of the RC time constant is significantly larger than the periodic time of the input signal.
To put it simply, we want RC to be much greater than T, typically around 10 times greater.
What this means for us is that the magnitude of the output voltage which is inversely proportional to RC, will end up being quite small when we look at the differences between its high and low voltage levels.
This results in a significant attenuation of the output voltage.
The reason behind this is that the capacitor has considerably less time to charge and discharge between each pulse.
However, we will see that the average output DC voltage tends to be around half as high as our input voltage.
In our earlier example with pulses, this would translate to an output of 5 volts (which is half of 10 volts).
Using an RC Integrator Circuit as a Sine Wave Generator
As we have seen above, an RC integrator circuit is quite capable of performing the integration operation by taking in a pulse input.
This results in an output that features a ramp-up and ramp-down effect, creating a triangular wave.
Now let us investigate what might transpire if we were to reverse this process and instead apply a triangular waveform to the input.
Would we then end up with a pulse or perhaps a square wave output?
When we feed a pulse-shaped input signal into our RC integrator circuit, the output transforms into a triangular wave.
However when we switch things up and apply a triangular wave as the input, the output changes character entirely and becomes a sine wave, amazing isn’t it?
This transformation occurs because of the integration over time of the ramp signal.
There are numerous methods available for generating a sinusoidal waveform, but one particularly straightforward and cost-effective way to achieve this electronically is by utilizing a pair of passive RC integrator circuits hooked up in series, as illustrated in the below given diagram.
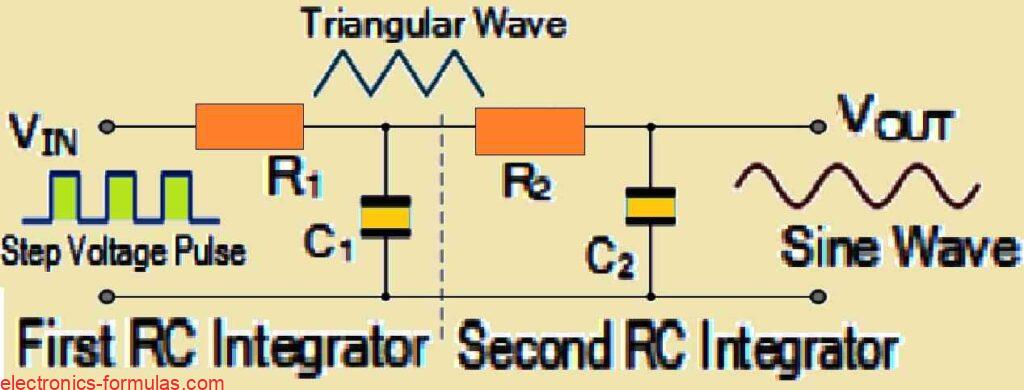
In the above diagram we can see that the first RC integrator takes our original pulse-shaped input and transforms it into a ramp-up and ramp-down triangular waveform.
This newly created triangular waveform then serves as the input for our second RC integrator circuit.
What this second integrator does is quite amazing, it smooths out the sharp points of the triangular waveform, effectively rounding them off and converting it into a sine wave.
This process is essentially like performing a double integration on the original input signal, with the RC time constant playing a crucial role in determining how much integration occurs.
Now it is important for us to note that when we integrate a ramp signal, we end up with a sine function. In simpler terms, this means we are essentially rounding off the triangular waveform.
The periodic frequency of this resultant sine wave, measured in Hertz, will be equal to the period T of our original pulse input.
Additionally let us consider what happens if we do the opposite and use a sine wave as our input signal instead.
In this case, the circuit will not function as an integrator, rather, it will behave like a simple low-pass filter (LPF).
Since the sine wave is a pure waveform it does not alter its shape in this process, instead, it just affects its amplitude.
Conclusions
From this tutorial so far, we have learned that the RC integrator essentially functions as a series RC low-pass filter circuit.
When we apply a step voltage pulse to its input, it generates an output that is directly proportional to the integral of that input.
This relationship provides us with a standard equation: Vo = ∫Vidt, where Vi represents the signal we feed into the integrator and Vo is the output signal that we obtain after integration.
Now when we integrate that input step function, what we get is an output that takes on the shape of a triangular ramp function.
This triangular ramp has an amplitude that is actually smaller than that of the original pulse input.
The magnitude of this attenuation is determined by the time constant of the circuit.
Therefore we can see that the shape of our output waveform depends significantly on how the time constant of our circuit relates to the frequency, or the period of the input pulse.
When we talk about an RC integrator we always compare its time constant to the period T of our input signal.
If we have a long RC time constant, it will give rise to a triangular wave shape with a lower amplitude compared to our original input signal.
This happens because the capacitor does not have enough time to fully charge or discharge.
On the other hand if we have a short time constant, it gives the capacitor more opportunity to charge and discharge effectively, resulting in a more rounded output shape.
Now, here is where it gets interesting, if we connect two RC integrator circuits in parallel, what happens is that we achieve a double integration effect on our input pulse.
In this scenario the first integrator circuit takes that step voltage pulse and transforms it into a triangular waveform.
Then our second integrator circuit takes this triangular waveform and smooths out its sharp points, ultimately producing a sine wave output with a significantly reduced amplitude.
References:
Leave a Reply